Ответы
Ответ дал:
1
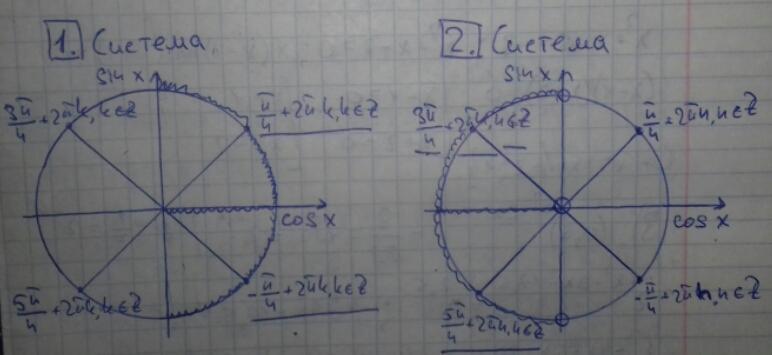
Решим системы через тригонометрический круг.
Наименьшим положительным решением будет x₁ = π/4 = 45°.
Наибольшим отрицательным решением решением будет x₂ = -π/4 = -45°.
Это можно определить, как по записи множества значений x, так и по точкам на круге, являющимися решением.
x₁-x₂ = 45°-(-45°) = 90°.
Ответ: 90°.
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
