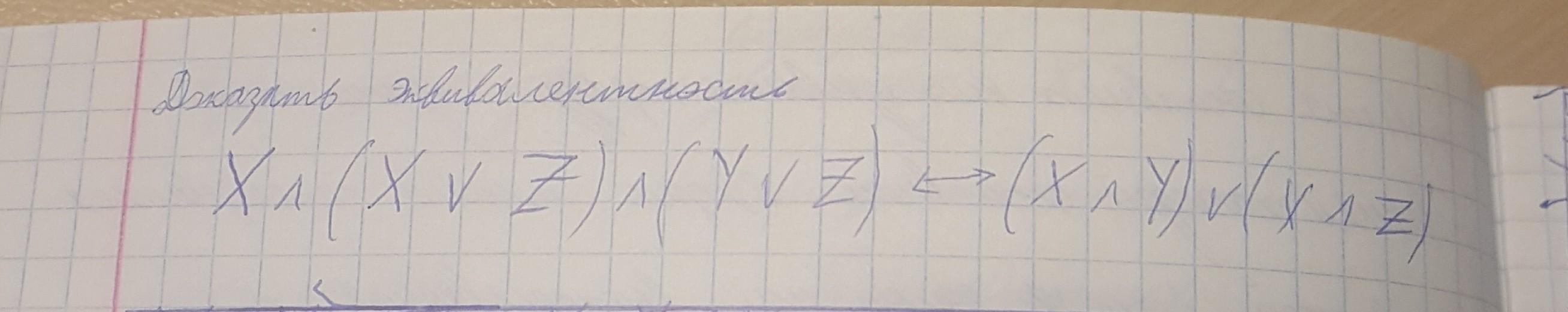Ответы
Ответ дал:
2
Преобразуем левую часть:
Используем закон поглощения:
Получается выражение
Преобразуем правую часть:
Используя закон распределения (справа налево), получаем:
В итоге получаем:
, слева и справа стоят одинаковые выражения. Доказано.
Эквивалентность действительно выполняется.
Ответ дал:
0
Х∩(Х∪Z)∩(Y∪Z)=X∩(Y∪Z)
При преобразовании левой части использовал закон математической логики, а именно закон поглощения.
(Х∩Y)∪(X∩Z)=X∩(Y∪Z)
При преобразовании левой части использовал распределительный закон.
Поскольку левая и правая части приведены к одному и тому же выражению, эквивалентность доказана.
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
8 лет назад