Question

Даны вершины треугольника А(2;8)  В(-1; 5) С(3;1) Вычислите косинусы углов треугольника

Answer 1

Ответ:

        cos∠B = 0

        cos∠A = 0,6

        cos∠C = 0,8

Объяснение:

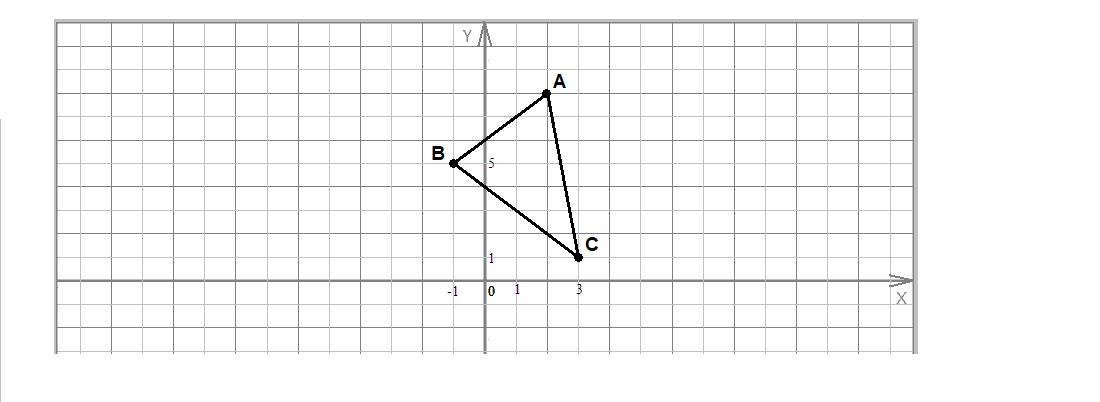
Найдем длины сторон треугольника по формуле расстояния между точками:

$d=sqrt{ (x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$

$AB=sqrt{ (2+1)^{2}+(8-5)^{2}}=sqrt{9+9}=3sqrt{2}$

$BC=sqrt{ (-1-3)^{2}+(5-1)^{2}}=sqrt{16+16}=4sqrt{2}$

$AC=sqrt{ (2-3)^{2}+(8-1)^{2}}=sqrt{1+49}=5sqrt{2}$

Проверим по теореме, обратной теореме Пифагора, не является ли этот треугольник прямоугольным:

AC² = AB² + BC²

(5√2)² = (3√2)² + (4√2)²

50 = 18 + 32

50 = 50 - равенство верно, значит треугольник прямоугольный с гипотенузой АС.

Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.

Косинус прямого угла равен нулю.

cos∠B = 0

cos∠A = AB / AC = 3√2 / 5√2 = 3/5 = 0,6

cos∠C = BC / AC = 4√2 / 5√2 = 4/5 = 0,8