решить уравнение..............................................................................
Приложения:
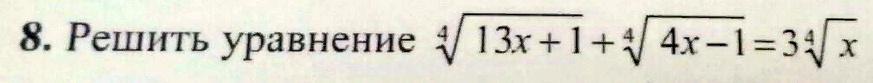
Ответы
Ответ дал:
3
Так как х = 0 не является корнем уравнения, то разделим обе части уравнения на х. Получим
Пусть , получим
Теперь выполним замену , тогда
(*)
Получаем, что сумма . Теперь упростим (*)
Квадратное уравнение относительно ab, тогда по т. Виета
Возвращаемся к обратной замене
Возводим обе части уравнения до четвертой степени
Это квадратное уравнение действительных корней не имеет, поскольку его дискриминант отрицательный.
Опять же возводим обе части уравнения до четвертой степени
По теореме Виета
Тогда
Отрицательный корень посторонний, т.к. ОДЗ уравнения x ≥ 1/4
Ответ: 1/3.
Аноним:
благодарю!
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад