Question

В круге проведена хорда длиной 16 дм, которая находится на расстоянии 6 дм от центра круга. Длина окружности равна ? дм;
π =3,14.

Answer 1

Ответ:

≈6,28 дм

Объяснение:

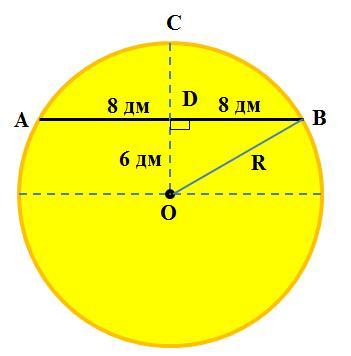
Дано (см. рисунок):

 Круг радиуса R

 AB=16 дм – хорда

 OD=6 дм - расстоянии от центра круга до АВ

 π≈3,14  

Найти L - длину окружности.

Решение. Диаметр или радиус, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Если из центра окружности провести перпендикулярный радиус ОС, радиус ОС делит хорду АВ пополам, то есть AD=DB=8 дм.

Теперь проведём радиус R=OB. Так как угол ODB=90°, то получим прямоугольный треугольник ODB с гипотенузой OB. Поэтому применима теорема Пифагора:

R²=OB²=OD²+DB²= 6²+8²=36+64=100=10²,

отсюда R=10 дм.

Длина окружности L=2·π·R≈2·3,14·10 дм=62,8 дм.