Найдите произведение всех корней уравнения
Приложения:

Аноним:
задавай вопросы на сайте иркмкис.топ отвечает сама администрация
Ответы
Ответ дал:
2
Ответ:
произведение корней уравнения равно -2.
Объяснение:
Приложения:
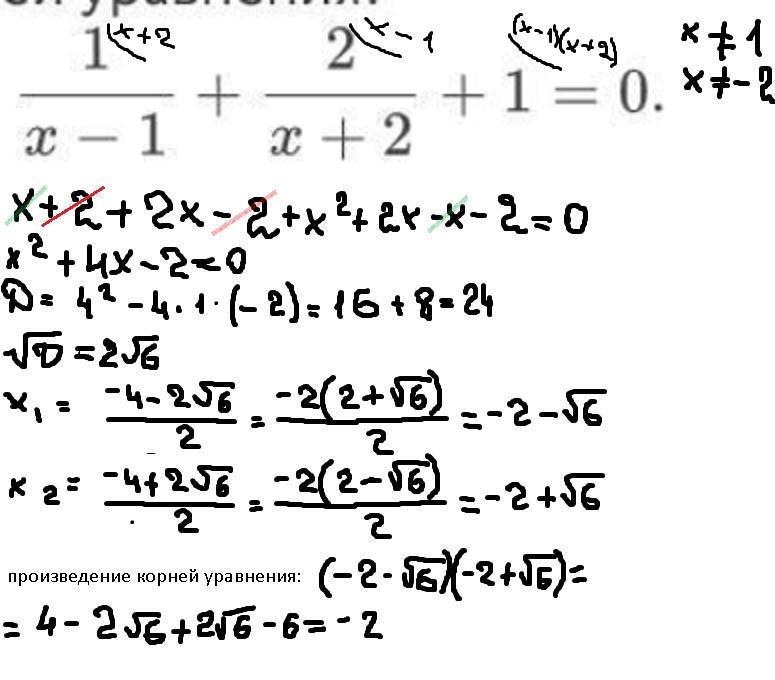
Ответ дал:
0
Ответ : -2
Вас заинтересует
1 год назад
2 года назад
3 года назад
3 года назад
9 лет назад