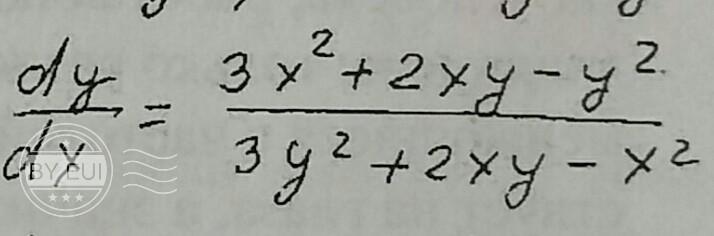Ответы
Ответ дал:
0
Данное дифференциальное уравнение является однородным. Пусть , тогда
, получаем
Последнее дифференциальное уравнение является уравнением с разделяющимися переменными.
Выполним обратную замену: u = y/x, получим общий интеграл
Вас заинтересует
1 год назад
1 год назад
1 год назад