Question

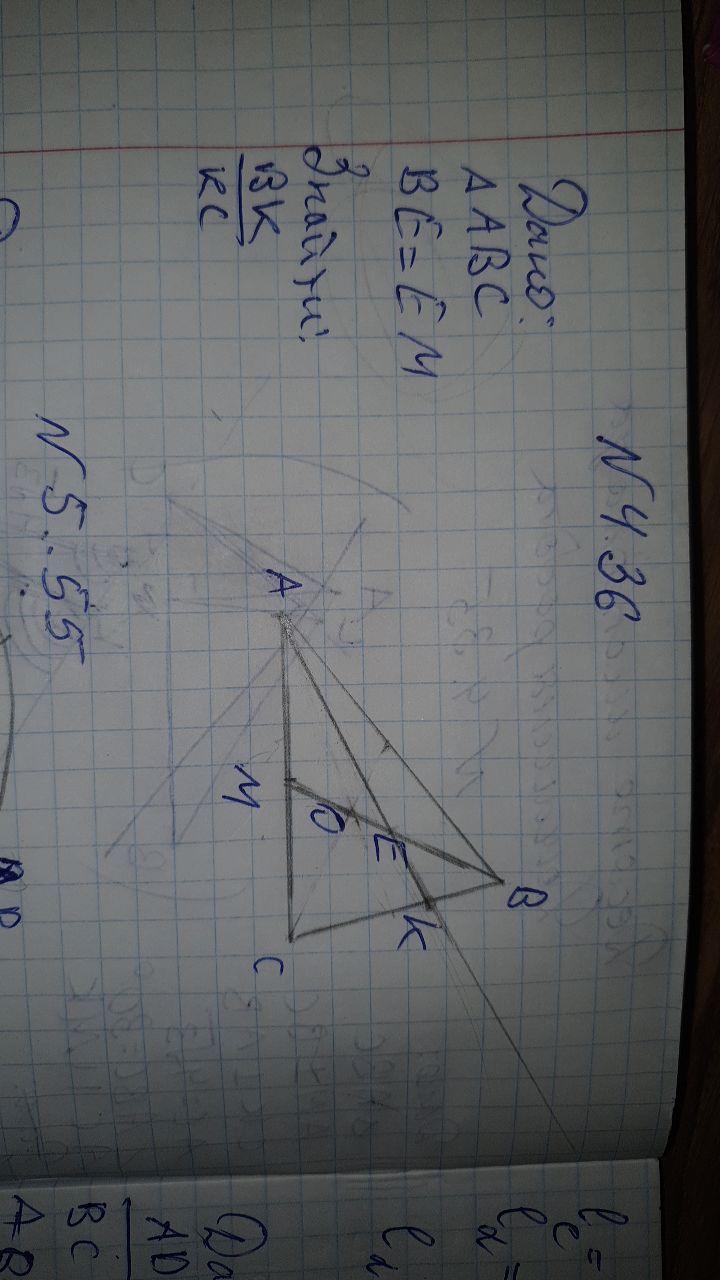
Треугольник ABC

BM - медиана, AM = MC

E - центр медианы, BE = EM

AE - прямая, рассекает сторону BC в точке K

Найти отношение BK/KC

Answer 1

По теореме Менелая

CK/KB *BE/EM *MA/AC =1

CK/KB *1 *1/2 =1 <=> KB/CK =1/2

Или

BD||AC

BED~MEA (по накрест лежащим углам при параллельных)

BD/MA =BE/ME =1

MA/AC=1/2 => BD/AC =1/2

BKD~CKA (по накрест лежащим углам при параллельных)

BK/CK =BD/AC =1/2