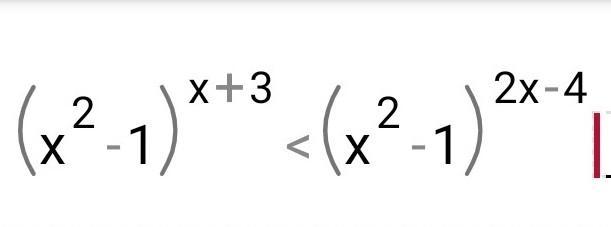Ответы
Ответ дал:
4
Так как обе части неравенства - это степени с одинаковым основанием, то решение неравенства зависит от значения основания степени.
1) Если a > 1 и aᵇ < aⁿ, то b < n; b,n∈R
2) Если a = 1 , то aᵇ = 1 ; b∈R
Получилось неверное неравенство, значит,
3) Если 0 < a < 1 и aᵇ < aⁿ, то b > n; b,n∈R
4) Если a = 0 , то aᵇ = 0 ; b∈R\{0}
Получилось неверное неравенство, значит,
5) Если a < 0, то возводить отрицательное число можно только в целую степень, то есть aᵇ имеет смысл при b∈Z.
Показатель степени (x+3) будет целым при любом целом значении x.
В этом интервале есть только одно целое число x=0. Проверка :
Объединив все полученные решения, получим
Аноним:
Как всегда превосходно :)
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад