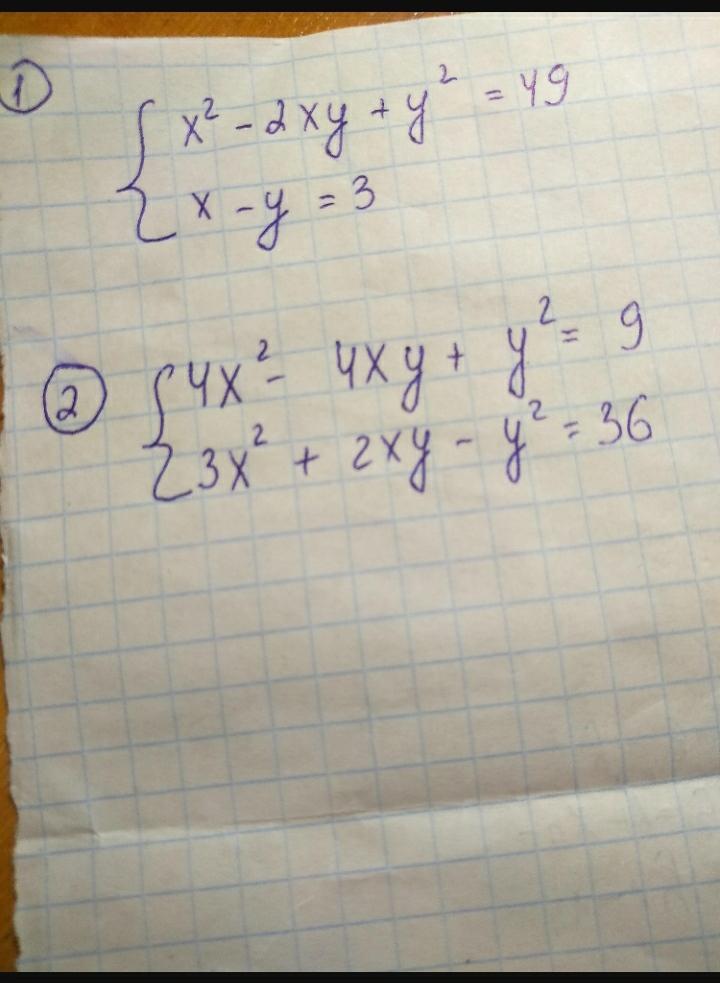Question

будь ласка поможіть СРОЧНО!!!!!!

Answer 1

$1)\; \; \left \{ {{x^2-2xy+y^2=49} \atop {x-y=3}} \right.\; \; \left \{ {(x-y)^2=49} \atop {x-y=3}} \right.\; \; \left \{ {{x-y=\pm 7} \atop {x-y=3}} \right.\; \; \Rightarrow$

Система не имеет решений, т.к. не может одно и то же выражение  (х-у) одновременно быть равным разным числам.

$2)\; \; \left \{ {{4x^2-4xy+y^2=9} \atop {3x^2+2xy-y^2=36}} \right.\; \; \left \{ {{(2x-y)^2=9} \atop {3x^2+2xy-y^2=36}} \right.\; \; \left \{ {{2x-y=\pm 3\qquad } \atop {3x^2+2xy-y^2=36}} \right. \\\\a)\; \; y=2x-3\\\\3x^2+2x(2x-3)-(4x^2-12x+9)=36\\\\3x^2+6x-9=0\; \; ,\; \; x^2+2x-3=0\; \; ,\; \; x_1=-3\; ,\; x_2=1\; (teorema\; Vieta)\\\\y_1=2\cdot (-3)-3=-9\; \; ,\; \; y_2=2\cdot 1-3=-1\\\\b)\; \; y=2x+3\\\\3x^2+2x(2x+3)-(4x^2+12x+9)=36\\\\-5x^2-6x-9=0\; \; ,\; \; 5x^2+6x+9=0\\\\D/4=9-45=-36<0\; \; \Rightarrow \; \; x\in \varnothing \\\\Otvet:\; \; (-3,-9)\; ,\; \; (1,-1)\; .$