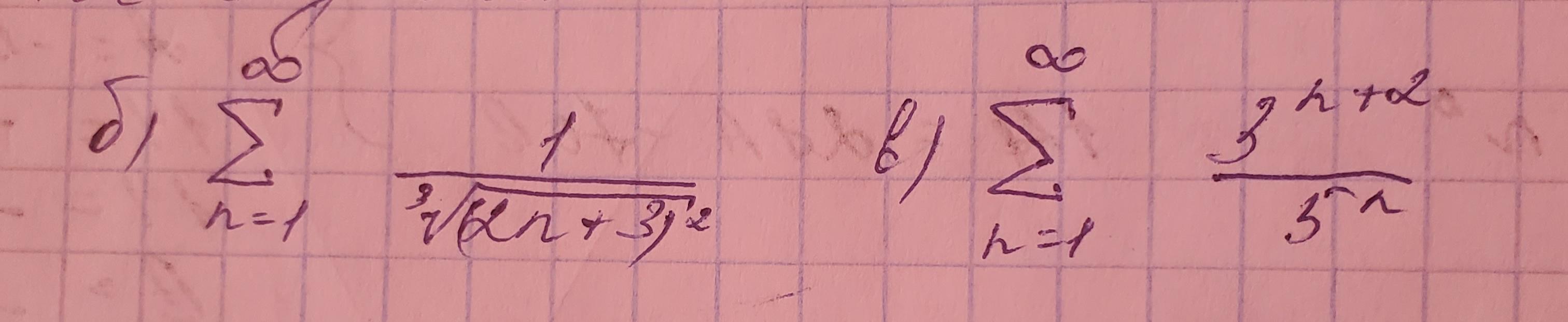Ответы
Ответ дал:
0
//////////////////////////////
Приложения:

Камила1211:
в первом примере почему заменяем dn на dt/2?
Вы не умеете интегрировать ,я понял
Я сделал замену 2n+3=t после чего взял производную. 2dn=dt и выразил dn
Интегральный признак Коши использовал в первом,а во втором Предельный признак Коши
Ответ дал:
2
1) Используем признак сравнения с расходящимся рядом.
Так как расходящийся ряд является мажорантным, то и минорантный ряд
тоже будет расходящимся .
P.S. - расходящийся обобщённый гармонический ряд.
Хорошо показали расходимость в первом!
спасибо
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад