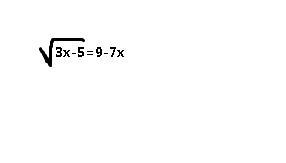Ответы
Ответ дал:
0
Ответ:
нет действительных корней
Объяснение:
1) Возведите обе части уравнения в квадрат:
2) Перенесите слагаемую в левую часть равенства:
3) Привести подобные члены, вычислить и поменять порядок слагаемых или множителей:
4) Изменить знаки:
5) Решить квадратное уравнение:
6) Раскрыть скобки. Вычислить:
7) Вычислить:
8) Выражение не определено на множестве действительных чисел:
х не принадлежит R
Ответ дал:
0
Ответ: уравнение не имеет корней.
помогите пожалуйста https://znanija.com/task/34005819
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад