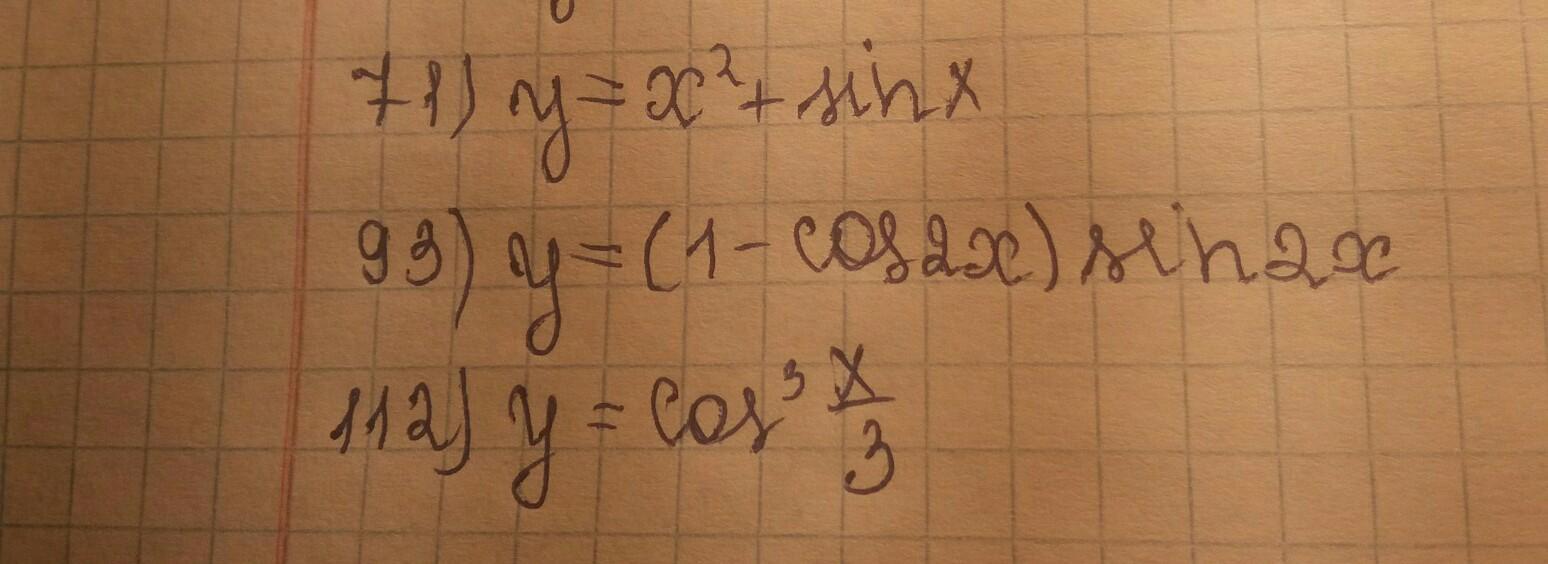Ответы
Ответ дал:
3
nikebod313:
Опечатка: 93) 4sin(3x)sin(x)
Ответ дал:
1
71)
93)
112)
Ответ:
там первое и второе чет изменятся не хочет
выдает ошибку
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад