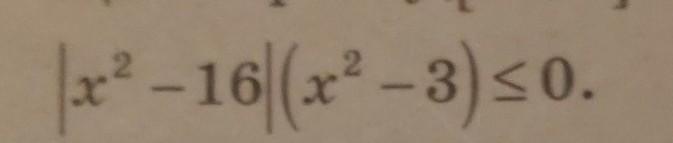Ответы
Ответ дал:
1
Решение задания приложено
Приложения:
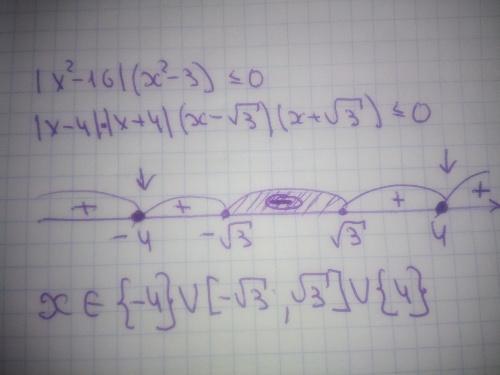
Аноним:
Вы поняли, почему + и + рядом?
А почему у вас так много заданий с модулями? Просто интересно.
Если честно, то не до конца
Много заданий из-за того, что пытаюсь освоить тему, но ничего не выходит.
Но, благодаря Вам, почти все получается решить
Смотрите, модуль числа (выражения) всегда значение неотрицательное. Поэтому если модуль ,как |х-4| или квадрат, как (х-4)^2, то именно в этой точке какой знак заходит справа, такой и выходит. Т. е на промежутках + и +, как в вашем примере неравенство принимает положительные значения. Видите стрелки? Это точки, которые принадлежат промежутку, они в фигурных скобках, так как неравенство нестрогое.
Вам нужно, чтобы кто-то хорошо объяснил метод интервалов вообще и с модулями в частности.
все темы легко даются, а вот эти модули лес для меня. Впринципе я понял почему + и + рядом.
На данный момент уже сложностей не испытываю
Вы все так хорошо объясняете и расписываете, что сложностей нету. )
Ответ дал:
1
Ответ:x∈[ ]∪{
}.
Объяснение:
Соответственно здесь важно знать, что произведение равно нулю, когда каждый из множетелей равен нулю, соотвественно приравниваем и считаем:
1) , используем формулу разности квадратов
2)
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад