Помогите, пожалуйста, решить неравенство ((log(16,4x^2)-log(sqrt(2*x),x/2))/(4log(16,1-x/3)+1)>log(2-2/3*x,x))
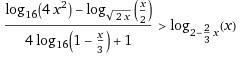
Ответы
Поехали:
Как обычно, начинаем с ОДЗ:
х > 0
х ≠ 0,5
х < 3
х ≠ 3/2
Таким образом наша ОДЗ:
(0;0,5) ∪(1/2; 3/2) ∪ (0,5;3)
Идем к уравнению. Приводим все к основанию 2:
Переносим всё в одну сторону, ищем общий знаменатель, производим действия типа log(2)[16] = 4:
Методом интервалов:
- + - + -
___________₀________₀________₀________₀_________
1/32 1/2 3/2 2
/////////////////// /////////////// ////////////////////
( - ∞ 1/32) ∪ (1/2; 3/2) ∪ (2; + ∞)
Подводим к нашему ОДЗ:
/////////////////////////////////////////////////////////////////////////////
____₀_______₀________₀________₀________₀______₀__________
0 1/32 1/2 3/2 2 3
/////////////////// /////////////// ////////////////////
Таким образом получаем:
х ∈ (0; 1/32) ∪ (1/2 ; 3/2) ∪ (2 ; 3)