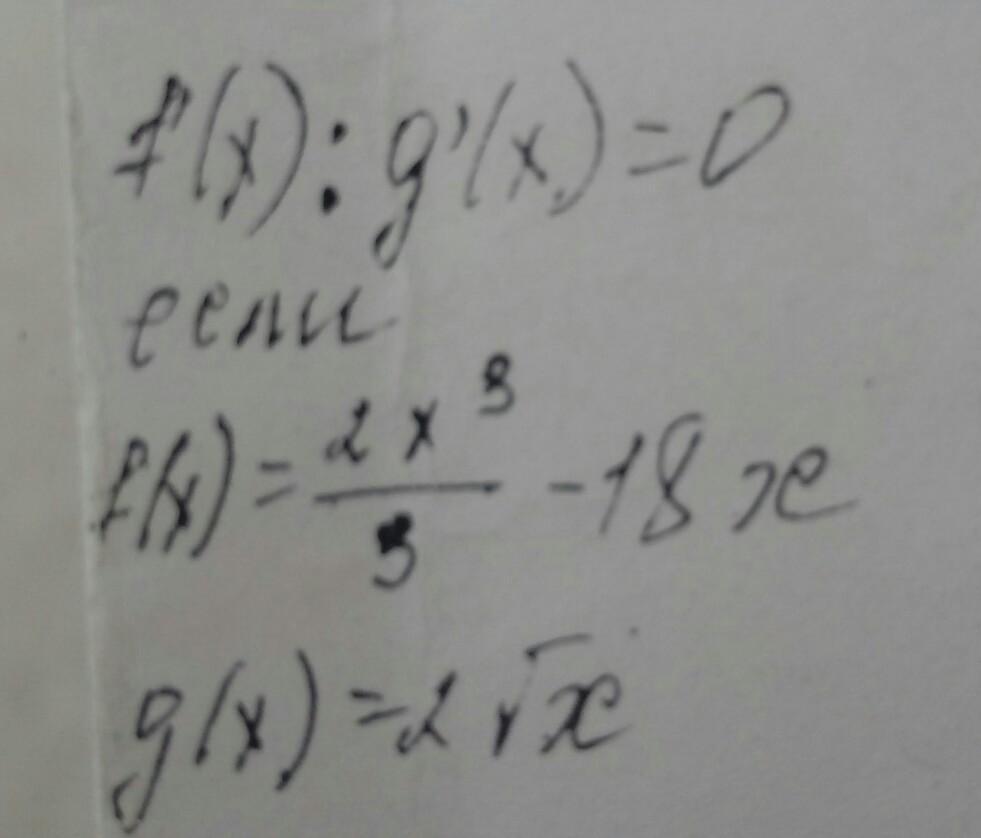Ответы
Ответ дал:
0
g`(x)=2*1/(2√x)=1/√x
f(x)/g`(x)=2/3*x^3√x-18x√x=0
x√x(2x^2/3-18)=0
x1=0
2x^2/3=18
2x^2=54
x^2=27
x=+-√27=+-3√3
Ответ x=-3√3;0;3√3
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
10 лет назад