Ответы
Ответ дал:
0
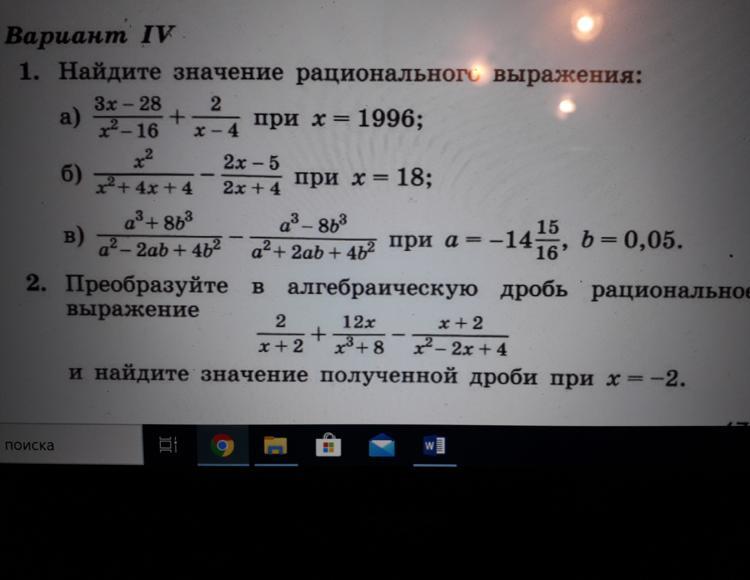
1. a)
b)
c)
2. Выражение при х=−2 не определено, т.к −2 не входит в область допустимых значений:
Все же, преобразуем выражение
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад