Question

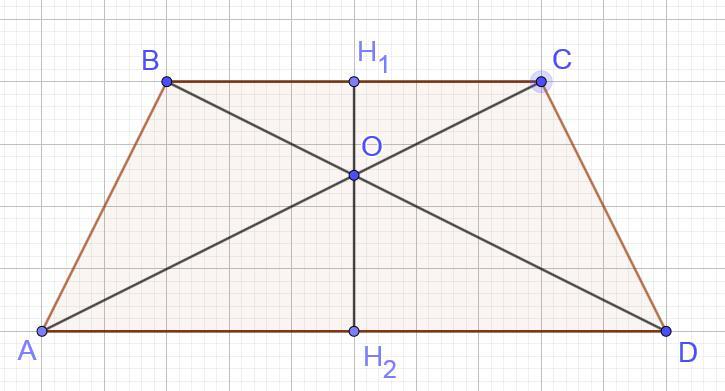
Точка перетину діагоналей рівнобічної трапеції віддалена від основ на 3 см і 5 см. Знайдіть площу трапеції, якщо більша основа дорівнює 20 см.

Answer 1

Задача: Точка пересечения диагоналей равносторонней трапеции отдалена от основ на 3 см и 5 см. Найдите площадь трапеции, если большая основа равна 20 см.

Решение:

Обозначим трапецию за ABCD, O — точка пересечения диагоналей, OH₁, OH₂ — отрезки, соединяющие O с основами трапеции, OH₁ = 3 см, OH₂ = 5 см. AD = 20 см.

Формула площади трапеции:

    $S=frac{a+b}{2} cdot h$,

где a, b — основы трапеции, h — высота трапеции.

Нужно найти высоту и меньшую основу трапеции.

Высота уже дана, и состоит и суммы длин отрезков, соединяющих точку пересечения диагоналей с основами.

    H1H2 (h) = OH₁+OH₂ = 3+5 = 8 (см)

Треугольники, образованные при пересечении диагоналей и лежащие на основаниях трапеции, подобные.

ΔOBC $sim$ ΔODA  ⇒  $frac{OB}{OD}= frac{OC}{OA}=frac{BC}{AD}$

Подобны и их внутренние элементы. Наши отрезки, соединяющие точку пересечения диагоналей с основами, являются высотами таких этих подобных треугольников. Используем их для нахождения коэффициента подобия:

    $k = frac{H_1}{H_2} = frac{3}{5}$

Подставим значения в пропорцию и найдем BC:

$frac{BC}{AD} = frac{3}{5}\\frac{BC}{20} = frac{3}{5}\\BC = frac{20cdot 3}{5} = 12 :: (cm)$

Подставим значения в формулу трапеции:

$S=frac{a+b}{2} cdot h\S=frac{20+12}{2} cdot 8 = 16cdot 8= 128 :: (cm^2)$

Ответ: Площадь трапеции равна 128 см².