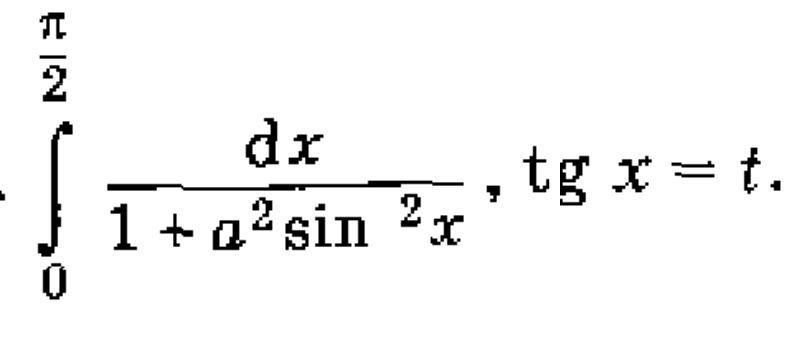Ответы
Ответ дал:
0
Ответ:
Объяснение:
Решим неопределенный интеграл:
Теперь решим неопределенный интеграл. Подставляя под тангенс, получим бесконечность. Значит мы имеем дело с несобственным интегралом 2 рода. Определим его сходимость:
Интеграл сходится.
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад