Question

Радиус основания цилиндра относится к его высоте как 1:2. Найдите

объём цилиндра, если диагональ его осевого сечения равна 8√2

Answer 1

Ответ: $128pi$

Пошаговое объяснение:

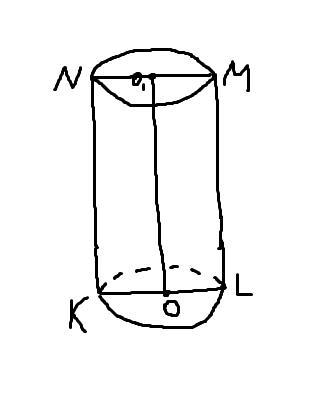
Осевое сечение цилиндра - это прямоугольник KLMN (диагональ KM). В прямоугольном треугольнике KLM по Теореме Пифагора: $KM^{2} =KL^{2}+ML^{2}$

Пусть радиус основания OL x, тогда LM 2x

$(8sqrt{2}) ^2=(2x)^2+(2x)^2\128=8x^2\x^2=16\x=4$

LM = 8

V = $pi r^{2} h$ = $pi$$*$16$*$8 = 128$pi$