Ответы
Ответ дал:
1
Объяснение:
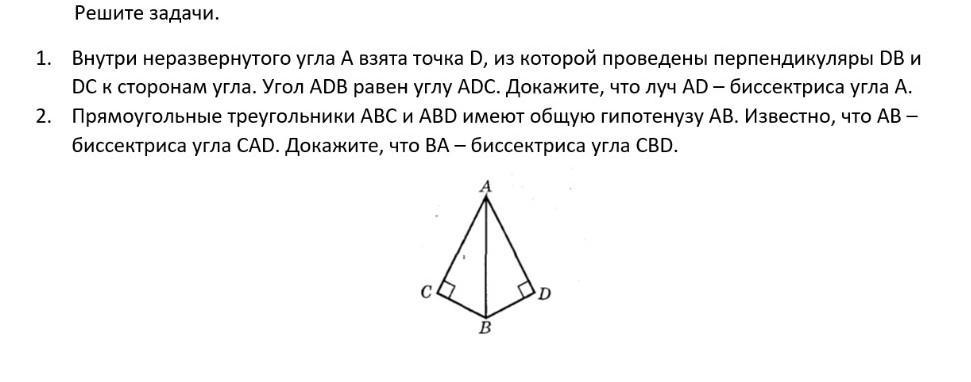
1)Дано ∠А-неразвернутый, D принадлежит внутренней области ∠А ,
∠ADB =∠ADC , DB ⊥AB , DC⊥ FC .
Доказать АD-биссектриса.
ΔDВА=ΔDСА как прямоугольные по гипотенузе и острому углу :DA-общая гипотенуза , ∠ADB =∠ADC по условию.
В равных треугольниках соответственные элементы равны:
DВ=DC⇒ точка D равноудалена от сторон угла, значит
АD-биссектриса.
2)ΔАСВ=ΔАDВ как прямоугольные по гипотенузе и острому углу:
ВA-общая гипотенуза , ∠САВ=∠DАВ , т.к АВ биссектриса .
В равных треугольниках соответственные элементы равны:
ВС=ВD. Учитывая что СB ⊥AС , ВD⊥ DА ⇒ точка В равноудалена от сторон угла, значит АВ- биссектриса угла ∠СВD
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад