Бічна сторона рівнобічної трапеції дорівнює 10 см, а радіус
вписаного в неї кола — 4 см. Знайдіть площу трапеції.
Ответы
Ответ дал:
9
Відповідь:
80 см²
Пояснення: S(КМРТ)
Дано: КМРТ - трапеція КМ=РТ=10 см, r=4 cм. Знайти S(КМРТ).
Проведемо висоти МА та РВ. МА=РВ=2r=8 cм
S(КМРТ)=(МР+КТ):2*РВ.
Якщо в трапецію можна вписати коло, то сума основ дорівнює сумі бічних сторін.
КМ+РТ=10+10=20 см, отже МР+КТ=20 см
S=20:2*8=80 см²
Приложения:
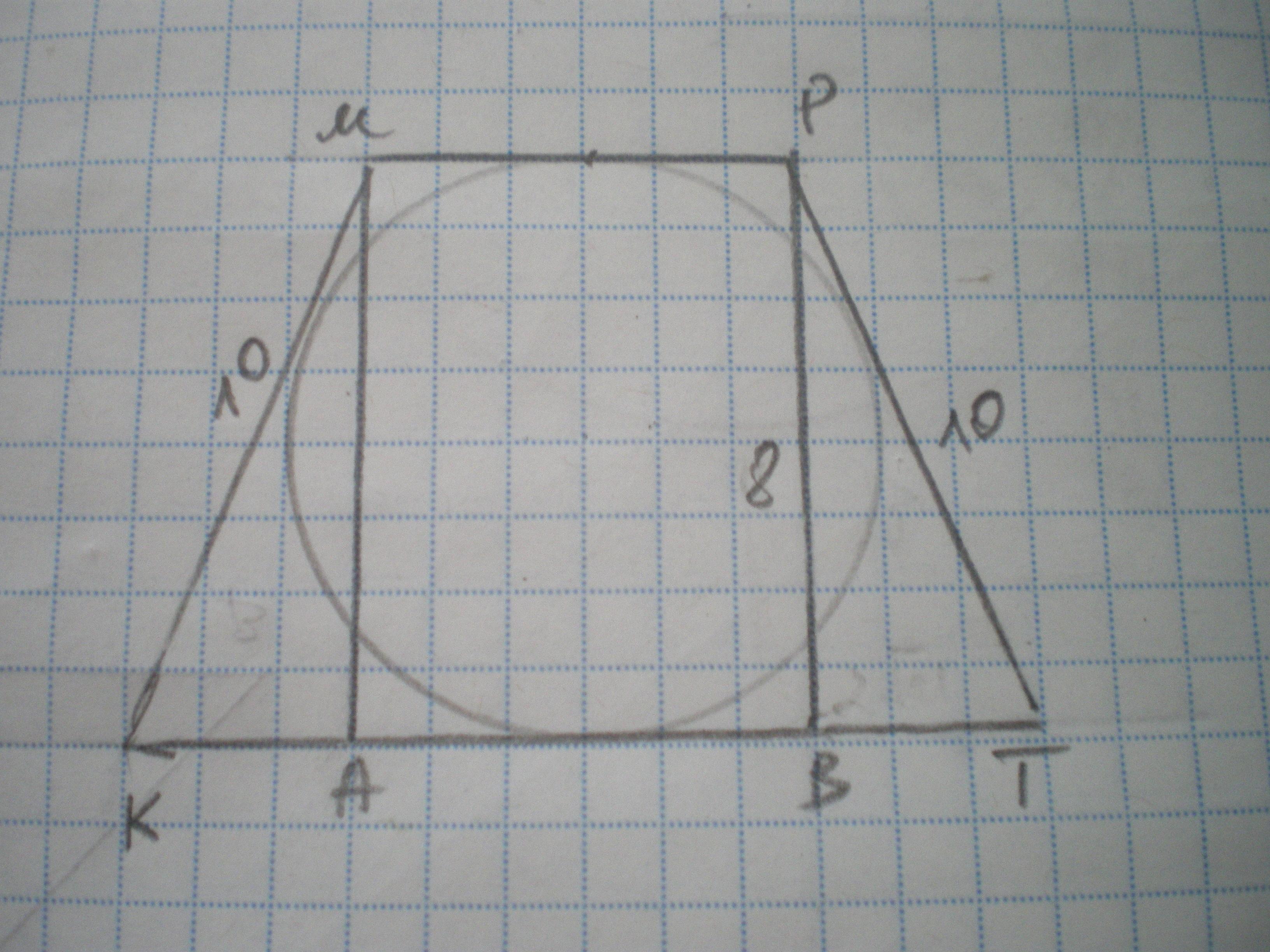
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад