найдите объем прямой призмы, в основании которой лежит треугольник со сторонами 2 см и 6 см и углом между ними 30о, если высота призмы равна 5 см.
Если можно с рисунком. СРОЧНО!!!
MultikTV:
Спасибо, за отметку.
Не за что)Вам спасибо
Ответы
Ответ дал:
7
Ответ:
призмы
см³.
Объяснение:
Обозначим данную призму буквами .
см.
см.
см.
=====================================================
призмы
осн.
см, по условию.
осн.
см².
призмы
см³.
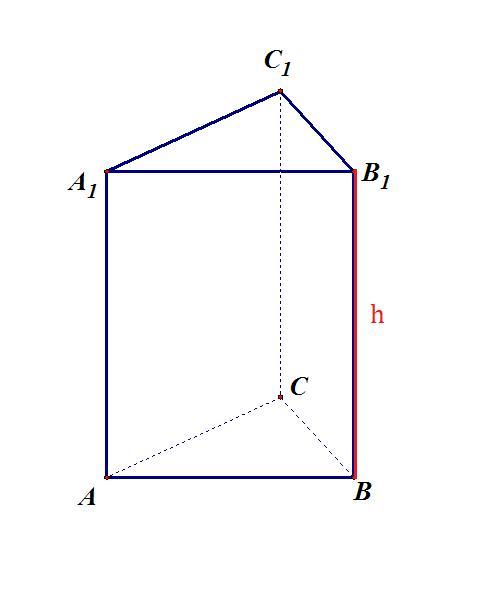
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад
8 лет назад