Ребят помогите ,пожалуйста отдаю все свои баллы
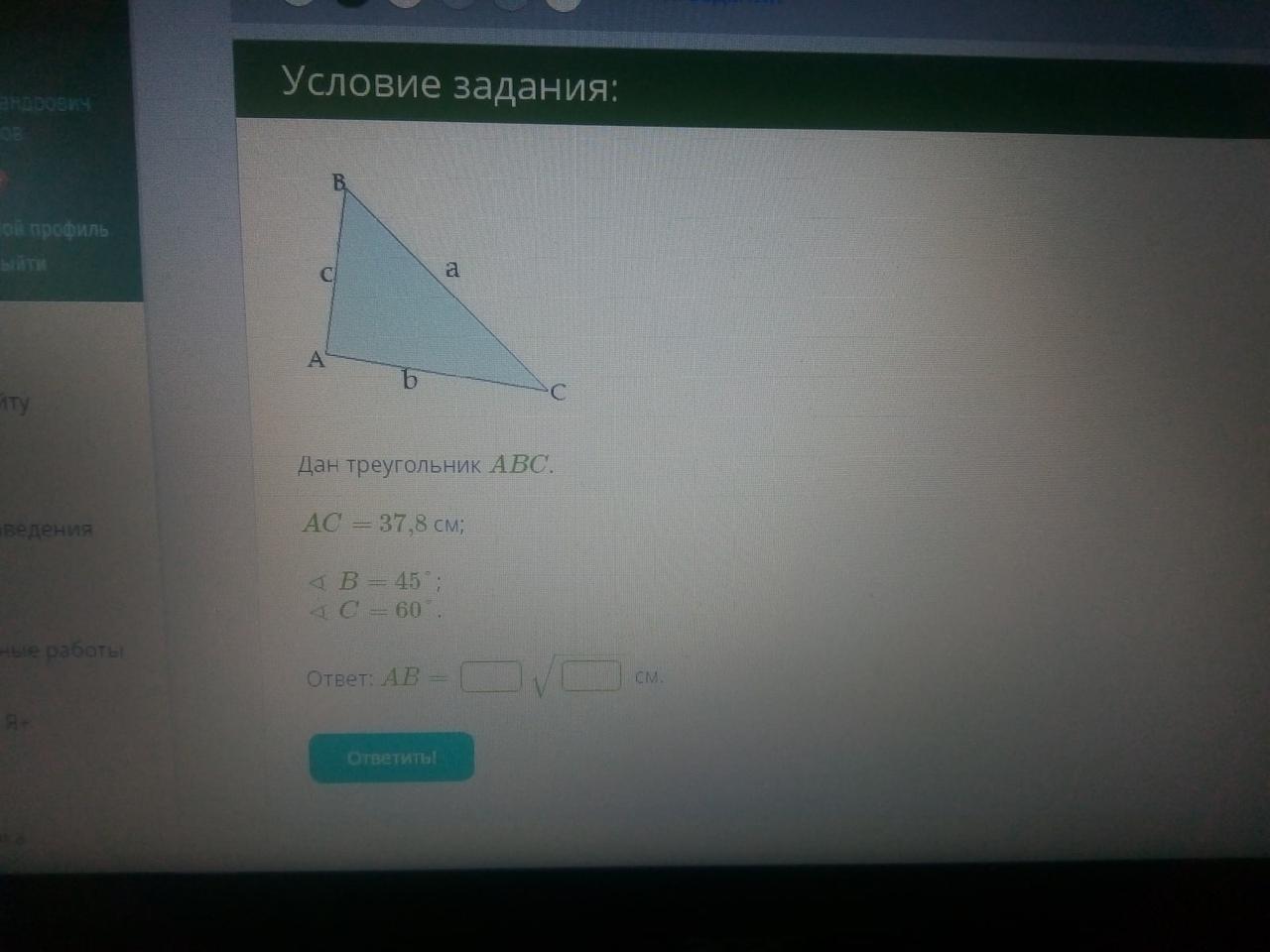
Дан треугольник ABC.
AC= 37,8 см;
∢ B= 45°;
∢ C= 60°.
Приложения:
exposer696:
я решил отмени
правильно?
Ответы
Ответ дал:
5
Ответ:
Объяснение:
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов:
Дано:
ΔАВС
∡B = 45°
∡C = 60°
AC = 37,8 см
________
АВ = ?
По т. синусов:
;
;
⇒
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад