В равнобедренной трапеции основания равны 6 см и 14 см, а боковая сторона равна 5 см. найти площадь этой трапеции.
Ответы
Ответ дал:
0
Рисуем трапецию АВСД
ВС = 6 см
АД = 14 см
АВ = СД = 5 см
Из вершины В опускаем высоту ВК.
АК = (АД - ВС) / 2 = (14 - 6) / 2 = 4 см
По теореме Пифагора высота
ВК = корень(AB^2 - AK^2) = корень(5^2 - 4^2) = 3 см
Площадь
S = (АД + ВС) * ВК / 2 = (14 + 6) * 3 / 2 = 30 кв. см
Ответ дал:
0
Так как трапеция равнобедренная, то AB=DC=5 см
EM=14-6=8cм⇒AE=MD=8÷2=4см
Теперь по Теореме Пифогора можем найти BE
AB²=AE²+EB²
BE=AB²-AE²(все под корнем)
ВЕ=5²-4²(всё под корнем)=√9=3 см
Sтрапеции=(BC+AD)÷2·BE
S=(6+14)÷2·3=30см²
Ответ: 30 см².
Приложения:
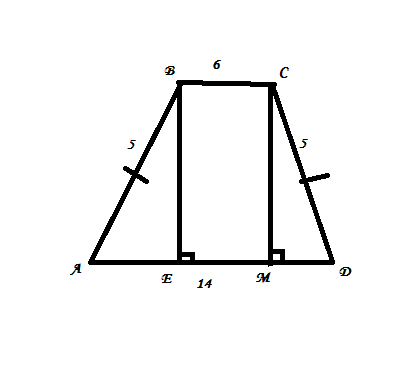
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад