Даю 35 баллов и 5 звезд!Найдите наибольшее и наименьшее значение функции f на указанном отрезке:
Приложения:
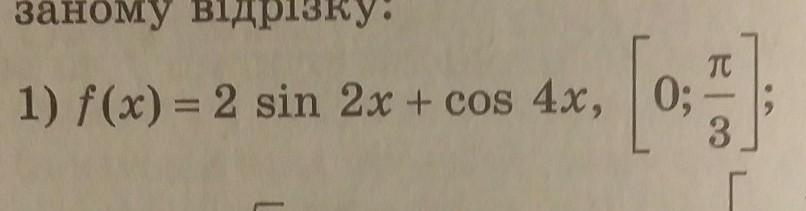
Ответы
Ответ дал:
1
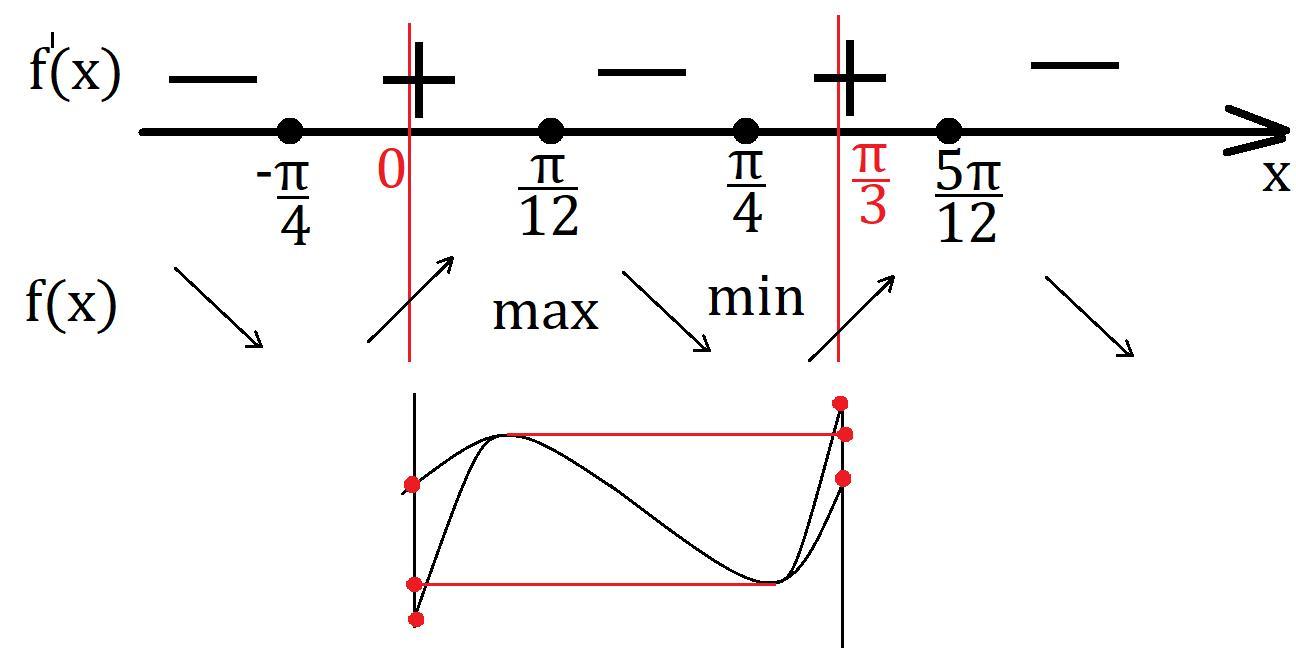
На координатной прямой разберёмся с промежутками монотонности функции на указанном отрезке.
Наибольшее значение или
.
f(наиб.) = 1,5
Наименьшее значение или
.
f(наим.) = 1
Ответ: 1 и 1,5.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад