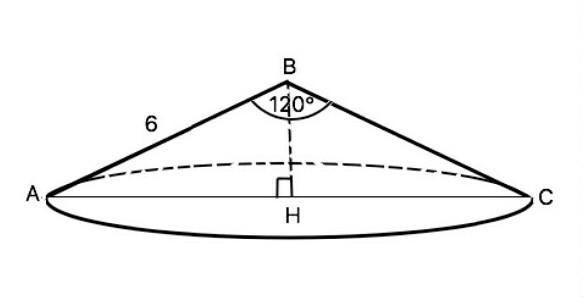
срочно!!!!!Осевое сечение конуса – равнобедренный треугольник с углом при вершине 120 и боковой стороной 6 см. Найти объем конуса.Дано и рисунок
Ответы
Дано:
Конус;
Осевое сечение конуса - равнобедренный △АВС;
∠В = 120°;
АВ = ВС = 6 см.
Найти:
V - ? (см³).
Решение:
Проведём высоту ВН. Получилось два равных прямоугольных треугольника АВН и СВН (их равенство можно также доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что △АВС - равнобедренный).
"Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является медианой и биссектрисой".
⇒∠АВН = ∠СВН = 120°/2 = 60°, так как ВН - биссектриса.
СН/СВ = sin ∠CBH ⇒ R = CH = CB ⋅ sin 60˚ = 6 ⋅ √3/2 = 3√3 (см).
Найдём высоту ВН, по теореме Пифагора:
с = √(a² + b²) ⇒ a = √(c² - b²), где a и b - катеты, c - гипотенуза.
a = √(6² - (3√3)²) = √9 = 3 (см).
Итак, ВН = 3 (см).
V = 1/3πR²h = π(1/3 ⋅ (3√3)² ⋅ 3) = 27π (см³).
Ответ: 27π (см³).