ПОМОГИТЕ ХОТЯ БЫ 1 РАЗ!!:(
объём прямоугольного параллелепипеда равен 16 боковое ребро 4 Найдите острый угол между диагоналями основания, если диагональное сечение паралелопипеда Квадрат.
orjabinina:
V(прям.пар.)=S(осн)*h. . 16=S(осн)*4 . S(осн)=4 . Т.к. диагональное сечение квадрат,то боковое ребро =диагонали основания.
ПРИВЕТ. Хотела помочь , но не успеваю. Да и вычисления какие-то огромные. Может где то ошиблась. Если никто не сделает, то в 12 часов посмотрю.............................................
В основании -прямоугольник. Пусть меньшая сторона-а , а>0, большая сторона-в ,в>0 . S(осн)=4 ⇒а*в=4 , а=4:в.
По т. Пифагора а²+в²=4² или (4\в)²+в²=16. Умножим обе части на в², получим 16+(в²)²=16в² или (в²)²-16в²+16=0 ⇒в=2√(1-√3) или в=2√(1+√3) учитывая в>0, а>0 ⇒ а=2\√(1-√3) , а=2\√(1+√3)
В основании -прямоугольник. Пусть меньшая сторона-а , а>0, большая сторона-в ,в>0 . S(осн)=4 ⇒а*в=4 , а=4:в.
По т. Пифагора а²+в²=4² или (4\в)²+в²=16. Умножим обе части на в², получим 16+(в²)²=16в² или (в²)²-16в²+16=0 ⇒в=2√(1-√3) или в=2√(1+√3) учитывая в>0, а>0 ⇒ а=2\√(1-√3) , а=2\√(1+√3)
Привет. Дорешать?
Ответы
Ответ дал:
2
Ответ:
30°
Объяснение:
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту (боковое ребро).
V = Sосн. · DD₁
Sосн. = V / DD₁ = 16 / 4 = 4
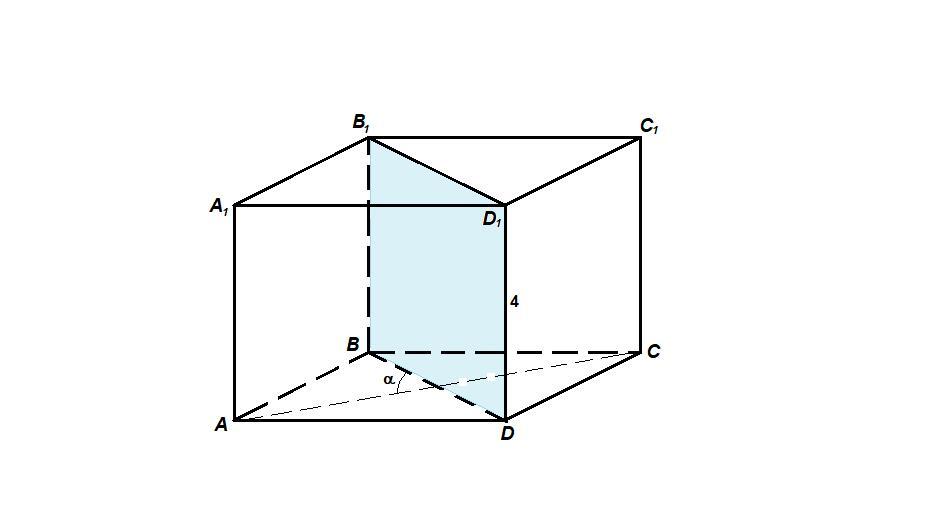
Диагональное сечение BB₁D₁D - квадрат, значит
BD = DD₁ = 4
Основание - прямоугольник.
Площадь прямоугольника через диагонали:
Sосн. = 1/2 BD · AC · sinα
Диагонали прямоугольника равны.
Sосн. = 1/2 BD² · sinα
4 = 1/2 · 4² · sinα
sinα = 4/8 = 1/2
α = 30°
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад