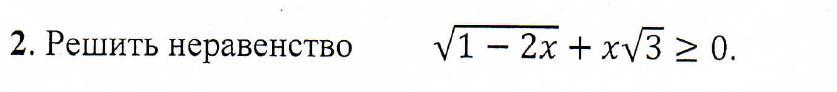Ответы
Ответ дал:
0
Ответ:
,.............
Объяснение:
................
Приложения:
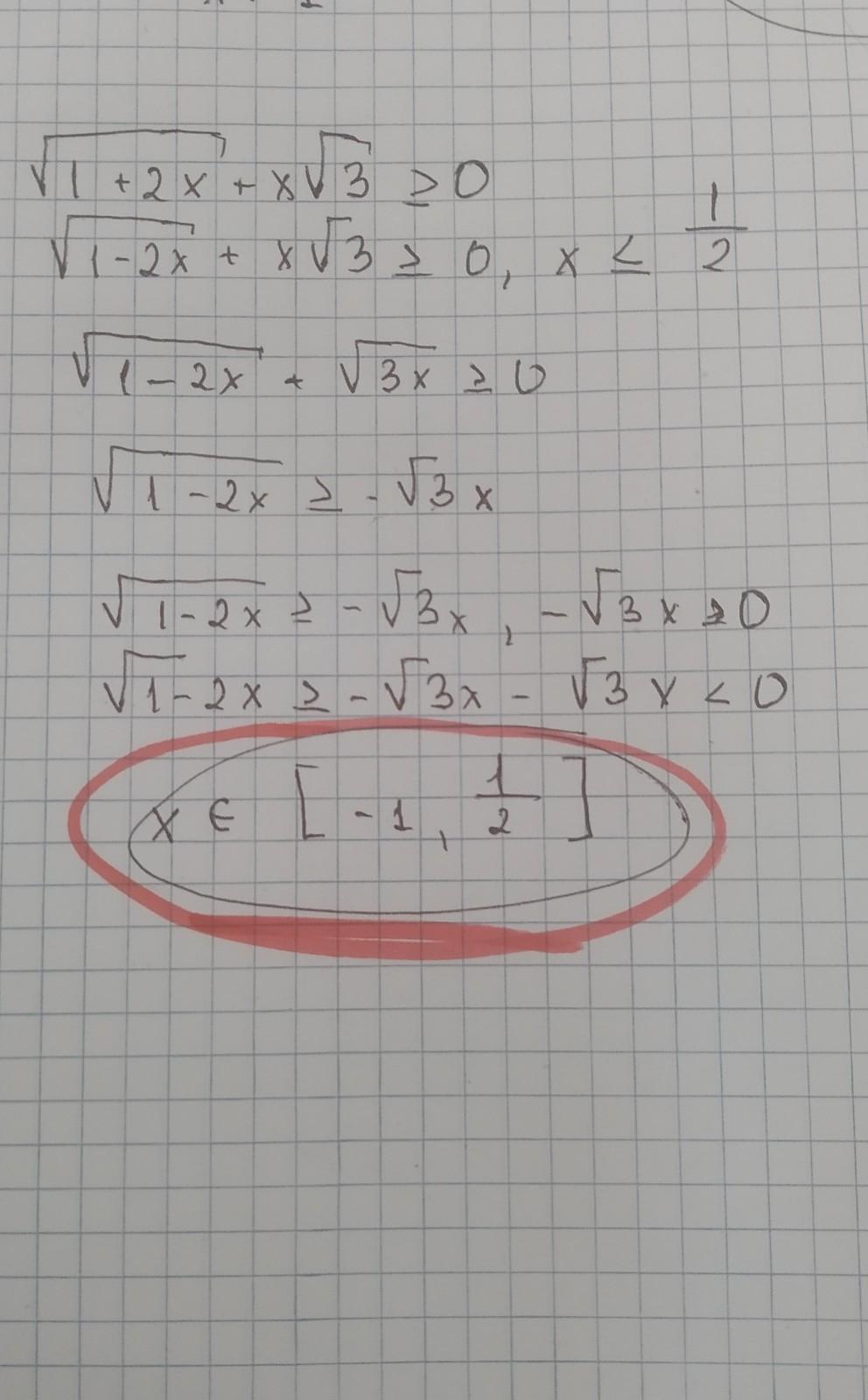
Ответ дал:
0
Объяснение:
ОДЗ:
-∞__+__-1__-__1/3__+__+∞
x∈[-1;1/3].
Ответ: согласно ОДЗ [-1;0,5].
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад