Question

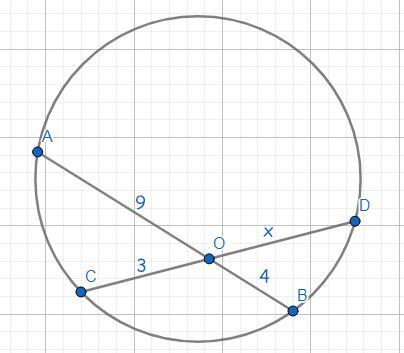
Хорды окружности AB и CD пересекаются в точке O. Если AO=9, OB=4 и CO=3, найдите длину хорды CD. (ответ 15, мне нужно объяснение)

Answer 1

Ответ:

15

Объяснение:

По теореме о произведении отрезков пересекающихся хорд AO*OB=CO*OD = > CD = AO*OB / CO = 9*4/3 = 12

Вся хорда равна CD = OD + CO = 12 + 3 = 15

Теорема звучит так : ""Если две хорды окружности пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.""

P.S. она доказывается через подобие треугольников

Answer 2

Обозначим OD за х.

Тогда, по теореме о пересекающихся хорд в окружности :

AO*OB = CO*OD

9*4 = 3*x

36 = 3*x

x = 36/3

х = 12

OD = x = 12

Вся хорда CD :

СD = СО + OD = 3 + 12 = 15.

Ответ : 15.