Question

Вычислите площадь фигуры, каждая точка которой удовлетворяет системе неравенств $\left \{ {{y\geq |x-1| +1} \atop {(x-1)^2 +(y-1)^2\leq 4}} \right.$

Answer 1

Ответ:

Ответ получается 2 см^2

Объяснение:

Мы должны понять, что это за графики

(1) Это график с модулем

(2) Это график окружности

Т.к. это система неравенства мы эти оба графика соединяем в один и смотрим пересечение.

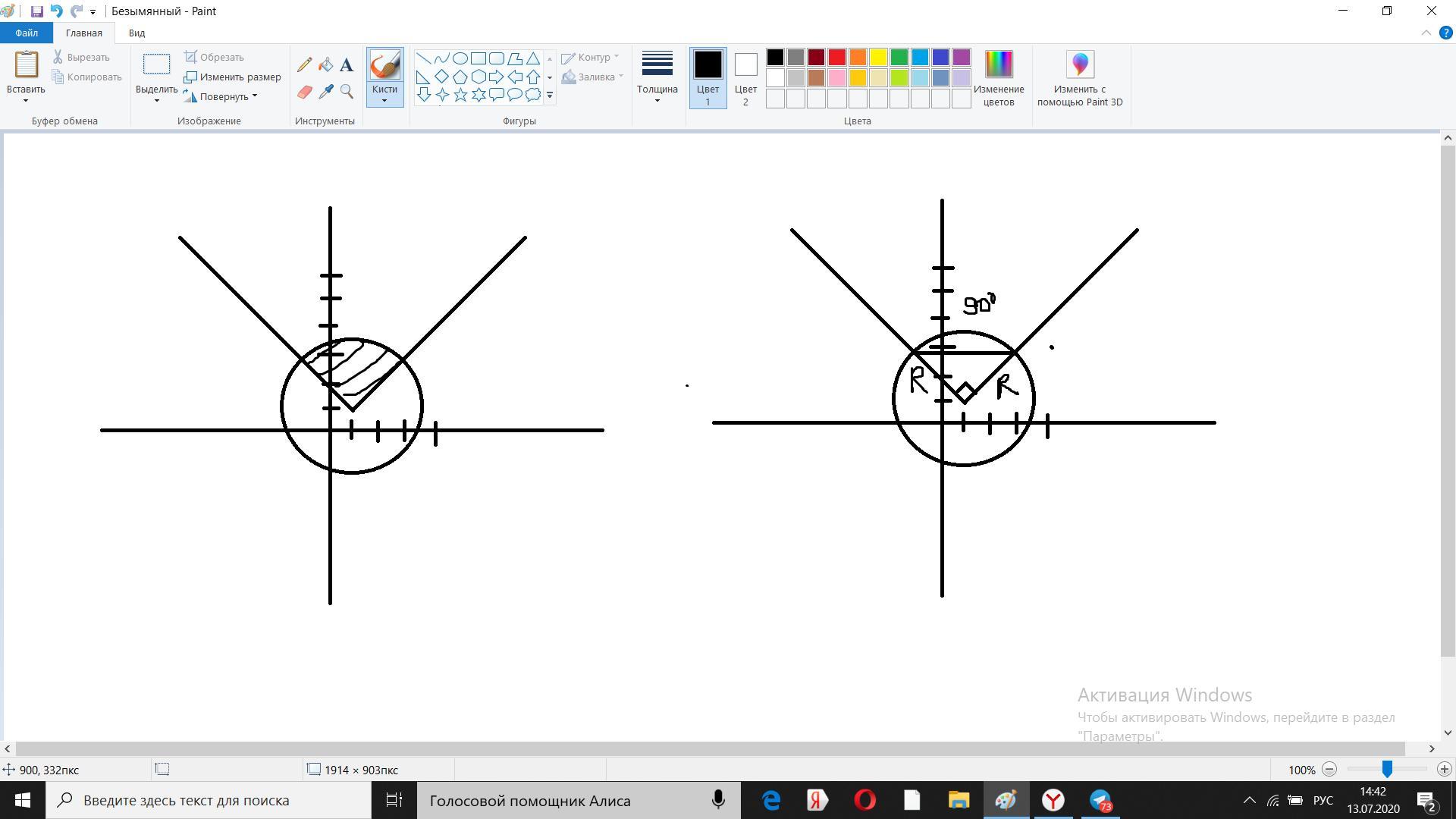
У нас сначала получился сектор, но т.к. сказано найти фигуру, то мы проводим хорду, которая будет являться гипотенузой равнобедренного(он равнобедренный из-за того, что его катеты это радиус окружности) прямоугольного  треугольника. Этот равнобедренный прямоугольник треугольник входит в сектор, который является промежутком этой системы неравенства.

По формуле окружности можно понять что R=2 см

Площадь тогда будет S= $\frac{1}{2} *2*2 = 2$ см^2

Answer 2

Ответ:

$D:\ \left\{\begin{array}{l}y\geq |x-1|+1\\(x-1)^2+(y-1)^2\leq 4\end{array}\right$

Область D ограничена кругом с центром в точке C(1,1) и  R=2 , а также  внутренней частью "уголка" - графика, полученного путём сдвига графика функции  $y=|x|$  на 1 единицу вправо вдоль оси ОХ и на 1 единицу вверх вдоль оси ОУ. Угол между линиями равен 90° . Значит заданная область D - сектор, равный четверти круга .

$S=\dfrac{1}{4}\cdot S_{kryga}=\dfrac{1}{4}\cdot \pi R^2=\dfrac{1}{4}\cdot \pi \cdot 2^2=\pi$  (кв.ед.)