Помогите пожалуйста срочно без спама
Приложения:
68tata:
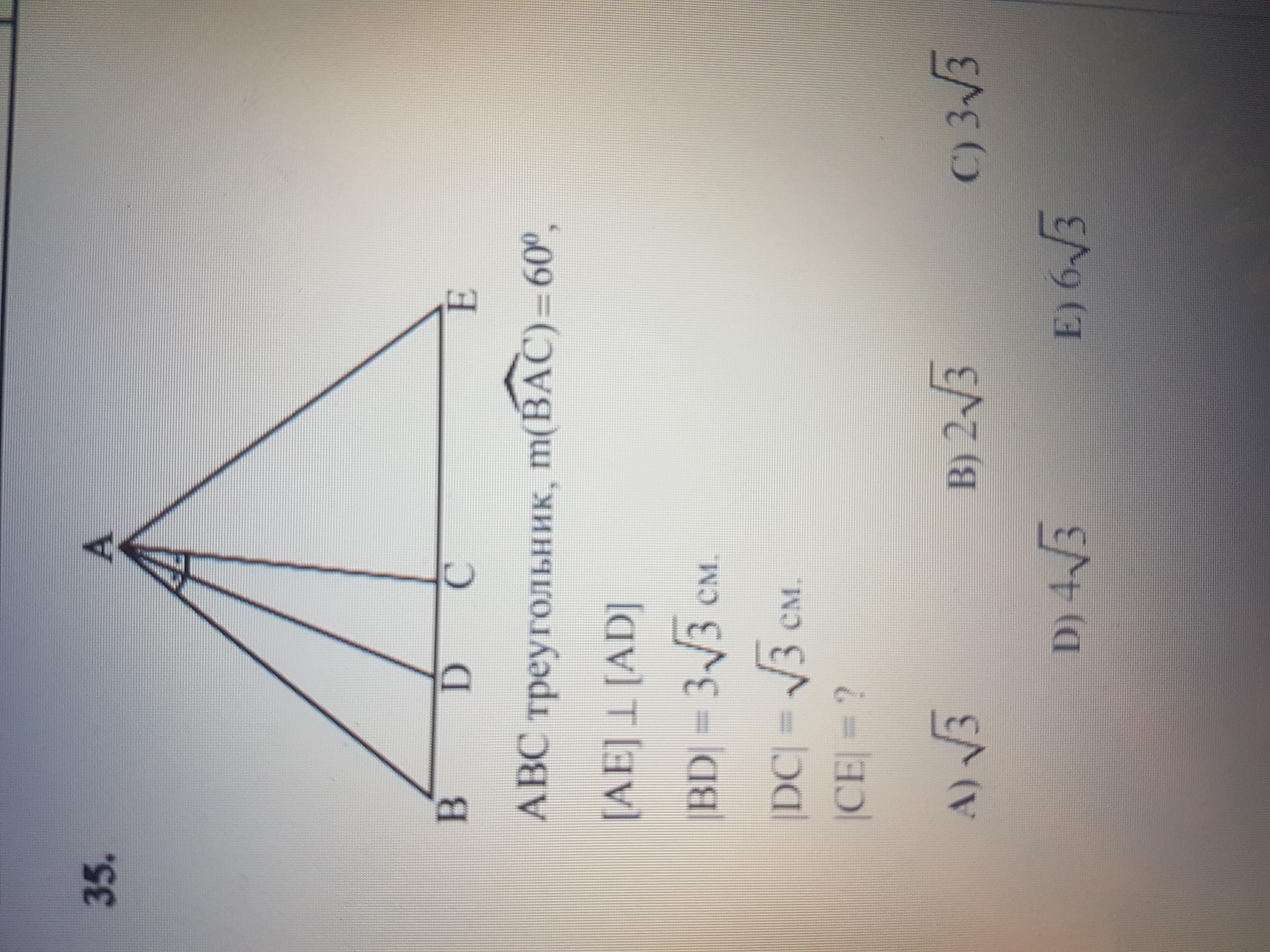
Из рисунка : угол ВАД=ДАС?
при условии, что AD-биссектриса, у меня получился ответ В)
Это точно биссектрисы- так обозначают на турецком языке- мальчик сегодня писал в другой задаче
задача интересна тем, что в получившемся квадратном уравнении возможны два решения и одно из них нужно еще доказать, что будет посторонним))
напишите кто-то решение, я дошла до половины, найдя АВ, АД,АС
Ответы
Ответ дал:
1
Ответ: CE=2*sqrt(3)
Объяснение:
AD- биссектриса угла ВАС=> AB/AC=BD/DC= 3:1
=> AB=3x AC=x BC=BD+DC= 3*sqrt(3)+sqrt(3)=4*sqrt(3)
По т косинусов:
BC^2=AB^2+AC^2-2*AC*AB*cos (BAC)
9x^2+x^2-2*3x^2/2=48
7*x^2=48
x^2=48/7
x=sqrt(48/7) => AC= sqrt(48/7) AB=3*sqrt(48/7)
Найдем синус В по т синусов
AC/sinB=BC/sin(BAC)
sqrt(48/7)/sinB=4*sqrt(3)*2/sqrt(3)= 8
sinB= sqrt(48/7)/8
cosB = sqrt (1- 48/7/64)= sqrt(1-6/56)=sqrt(1-3/28)= 5/sqrt(28)
sinE= sin (180-B-A)=sin(B+A)= sinB*cosA+cosB*sinA
A= DAE+BAD=90+30=120
sinA=sqrt(3)/2 cosA=-1/2
sin E= sqrt(3)/sqrt(7)
А теперь из треугольника АСЕ по т синусов находим СЕ
CE/sin (CAE)=AC/sinE
CE/sin60= sqrt(48/7)/sqrt(3)*sqrt(7)
CE*2/sqrt(3)=4
CE=2*sqrt(3)
Вас заинтересует
2 года назад
2 года назад
2 года назад
9 лет назад