Question

Дуже потрібно!!!!!!!!!до п‘ятниці!!!!!!

Answer 1

10.

$\left\{ {{x^{2}-x-12\leq0}\atop{3x-2>0}}\right.$

1. Найдём корни неравенства х² - х - 12 ≤ 0

Для этого приравняем его к нулю и решим с помощью дискриминанта:

х² - х - 12 = 0

D=(-1)² - 4×1×(-12)=49

$x_{1}=\frac{-(-1)+\sqrt{49}}{2}=4$

$x_{2}=\frac{-(-1)-\sqrt{49}}{2}=-3$

С помощью метода интервалов (см.скрин1) получим:

х ∈ [-3;4]

2. Решим неравенство 3х-2>0 :

3х-2>0

3х>2

$x>\frac{2}{3}$

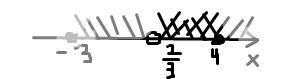
3. Нам необходимо, чтобы неравенство и уравнение имели общее решение. С помощью метода интервалов (см.скрин2) получим:

х ∈ (2/3; 4]

Ответ: х ∈ (2/3; 4]

11. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон

Пусть х - меньшая диагональ, причём х>0. Тогда из условия х+6 - большая диагональ.

Составим уравнение и решим его:

х² + (х+6)² = 7² + 9² + 7² + 9²

x² + x² + 12x + 36 = 49×2 + 81×2

2(x² + 6x + 18)=2(49+81)

x² + 6x + 18 = 49 + 81

x² + 6x + 18 - 49 - 81 = 0

x² + 6x - 112 = 0

D = 36 - 4×(-112)=484

$x_{1}=\frac{-6+22}{2}=8$

$x_{2}=\frac{-6-22}{2}=-14$

x₂<0 ⇒ x=8 ⇒ x+6=14

Откуда диагонали равны 8 см и 14 см.

Ответ: 8 см и 14 см

Answer 2

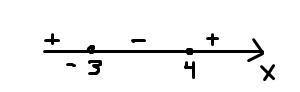
Відповідь:

10)х∈ (2/3;4]

11) 8 см, 14см

Покрокове пояснення:

в файлі