Question

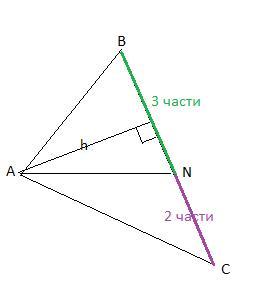
В остроугольном треугольнике ABC проведена прямая AN, делящая сторону BC в отношении 2:3, считая от вершины C. Чему равна площадь ABC, если площадь треугольника ABN равна 15?

Answer 1

В остроугольном треугольнике ABC проведена прямая AN, делящая сторону BC в отношении 2:3, считая от вершины C. Чему равна площадь ABC, если площадь треугольника ABN равна 15?

Объяснение:

ВС- 5 частей, BN-3 части ⇒ BN=3/5BC.

S(ABN)=0,5*h*BN==0,5*h*3/5BC

S(ABC)=0,5*h*BC.  Разделим 1 равенство на второе почленно :

S(ABN) : S(ABC)=0,5*h*3/5BC : (0,5*h*BC)  "посокращаем "

$\frac{15}{S(ABC)} =\frac{3}{5}$  ,

S(ABC)=$\frac{75}{3} =25$ (ед²)

Answer 2

Объяснение:см. во вложении