Биссектриса AD треугольника ABC равна отрезку DC, AC=2AB. Найдите величину угла ADB в градусах.
oganesbagoyan:
https://otvet /question/79716785
otvet.m ail.ru
Соединить и читать
https://otvetotvet.m ail.ru /question/79716785
otvet.m ail.ru/question/79716785
Ответы
Ответ дал:
16
Ответ:
60°
Объяснение:
Приложения:

Ответ дал:
7
https://znanija.com/task/37801426
Дано : ΔABC; ∠BAD =∠CAD (AD → Биссектриса) ; AD=CD ; AC=2AB - - - - - - - - - - - - - -
∠ADB - ?
Ответ: 60°
Объяснение: AD = CD ⇔ ∠С=∠CAD ; ∠ADB =∠С +∠CAD =2∠С ,
т.к. ∠ADB внешний угол ΔADC.
CD/BD =AC/AB (свойство биссектрисы)
СD/BD=2 ⇔ СD=2BD AD = CD = 2BD
! AD²= AB*AC - СD*BD ⇔ 4BD² =2AB² -2BD² ⇔3BD² =AB² ⇔
(2BD)²=AB²+BD² ⇔ AD²=AB²+BD² ⇒ ABD =90° (по обратной теореме Пифагора)
В ΔABC катет AB = половине гипотенузы AC ⇒ ∠С=30°
∠ADB =2∠С=60° . || ∠С = ∠A = 60° ; ∠B =90° ||
Приложения:
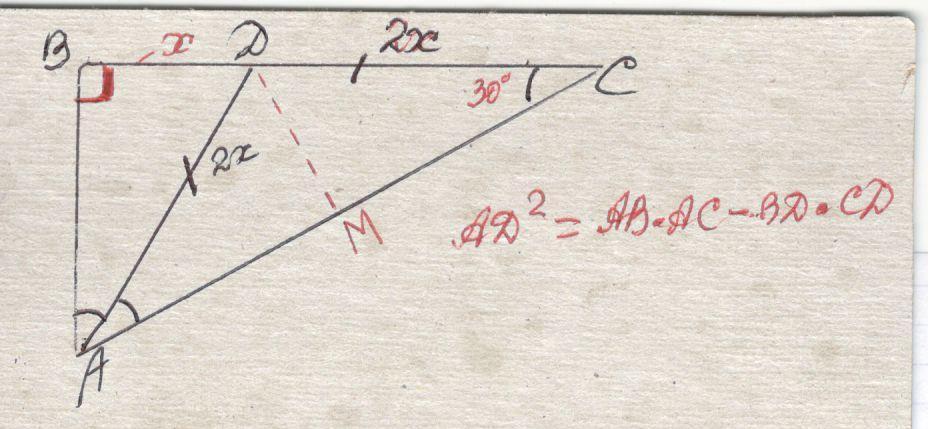
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад