Срочно 50 баллов.......
Приложения:
lidiasaraa3:
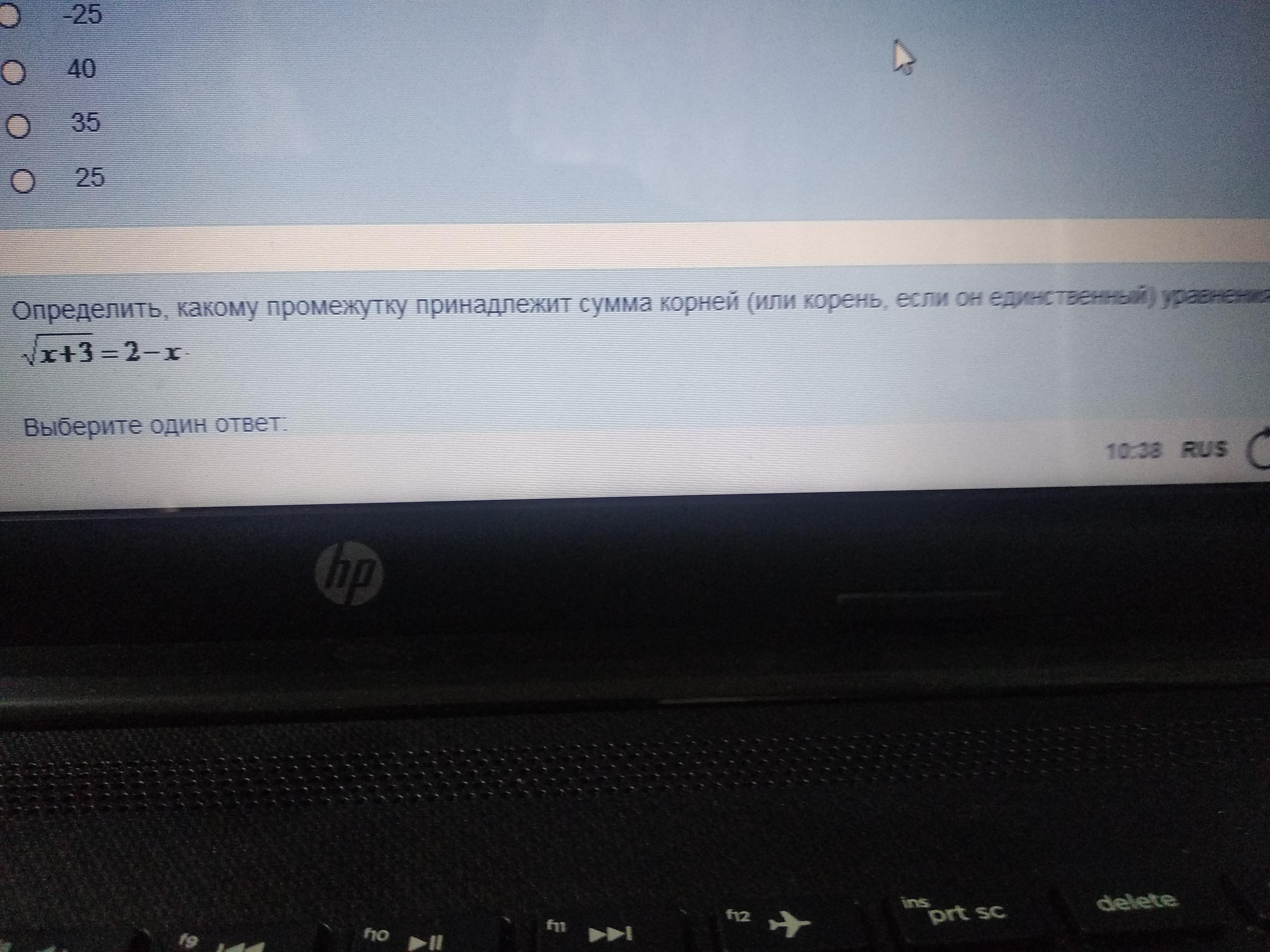
нужно же видеть эти промежутки
-6;4 . 2;3 . -1;0 0;1 4;6 какой из них?
Ответы
Ответ дал:
1
Ответ:
Сумма корней принадлежит промежутку 0,1
Объяснение:
Возведем левую и правую часть в квадрат.
x+3=x^2-4x+4
x^2-5x+1=0
D=25-4=21
x1=(5-sqrt(21))/2
x2=(5+sqrt(21))/2
Так как sqrt(21)<5, то каждый корень положительный. Поэтому подкоренное выражение в исходном уравнении больше нуля.
Так как правая часть должна быть положительной, то подходит только первый корень x1.
Корень из 21 это примерно 5×(1-4/50)=4.6
x1 примерно 0.2.
Вы лучшие ! Спасибо !!
х должен быть меньше 2, т.е.,корень один
Ошибся, ответ неправильный
Исправил, спасибо за замечание.
Спасибо большое!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Ответ дал:
1
Ответ.
Спасибо большое!!
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад