1.
Найдите все натуральные

, что число

- простое, состоящее из не более, чем
19 цифр.
2. см рис.
3.Докажите, что не существует натурального , при котором

делится на 101
Помогите пожалуйста хоть с чем-нибудь)
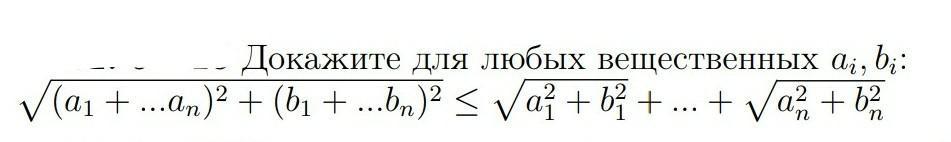
Ответы
Пусть простое число, большее 2 (если
, то
). Тогда
четно. Заметим, что
, случай с 18-ю уже очевидно не подходит. Возможные кандидаты: четные числа от 2 до 16.
Согласно малой теореме Ферма , вместе с тем
. Сложив оба сравнения, получим
, откуда ясно, что
. Эта процедура похожа на алгоритм Евклида. Повторив такую операцию еще несколько раз, получим
, где
определяется так:
. Но
, то есть
. Тогда
, противоречие.
Есть еще случай, когда, производя операцию (алгоритм Евклида), мы не приходим к 0 (попадаем в цикл). Это происходит тогда и только тогда, когда . Небольшая проверка дает
:
.
Ответ:
Представим себе последовательность прямоугольных треугольников в системе координат. Ровно один катет треугольника вертикален и ровно один горизонтален. Пусть каждый треугольник "цепляется" вершиной за предыдущий так, что гипотенузы треугольников образуют монотонно снижающуюся ломаную. Тогда неравенство очевидно: кратчайший путь есть отрезок между верхней вершиной первого треугольника в последовательности и нижней вершиной нижнего. Равенство достигается тогда, когда треугольники попарно подобны.
Предположим обратное.
Заметим, что все , такие что
не подходят. Поскольку 101 является простым, то
взаимно просто со 101. Значит,
.
Более того, согласно малой теореме Ферма . Значит, порядок числа
по модулю 101 делит как 3, так и 100, но 3 и 100 взаимно просты. Противоречие.