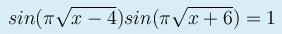Ответы
Ответ дал:
1
Ответ:
6.25
Объяснение:
Приложения:



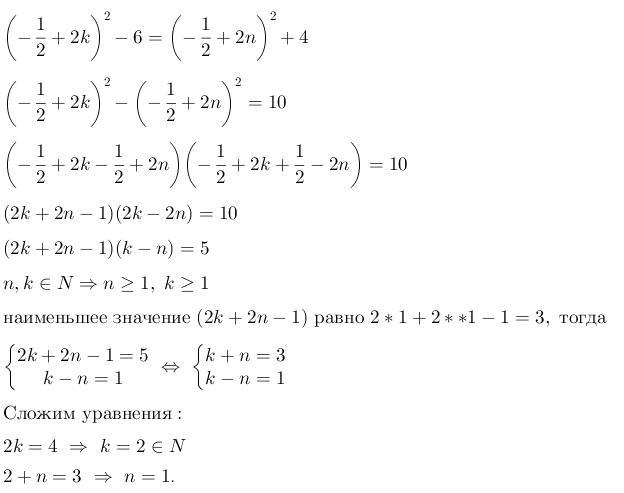
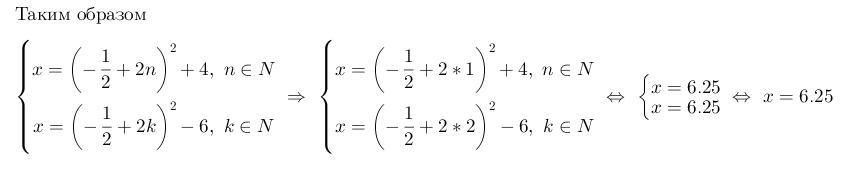
Ответ дал:
2
Ответ:
Объяснение:
Перейдем к системе:
Решим первое уравнение системы:
Заметим, что - отрицательное число, если
. Функция
возрастает на всей области определения, поэтому наименьшее значение она принимает при
:
. Единственное значение, которое принимает
на промежутке
- это
.
Тогда достаточно решить уравнение .
Решим уравнение:
Получим, что .
Теперь осталось проверить, будет ли этот корень являться корнем второго уравнения системы:
Значит - корень исходного уравнения.
Уравнение решено!
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад