Question

20. В равнобедренном треугольнике один из углов 120°, а его ос-
нование равно 16 см. Найдите высоту треугольника, проведенную
из вершины его острого угла.​

Answer 1

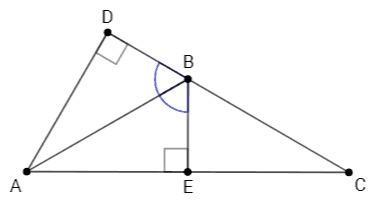
△ABC - равнобедренный, AC - основание.

AC= 16 см

Углы при основании равнобедренного треугольника острые. Следовательно, угол 120° противолежит основанию.

∠ABC= 120°

AD⊥BC

Найти AD

∠ABD= 180°-∠ABC =180°-120° =60°

BE⊥AC

В равнобедренном треугольнике высота является медианой и биссектрисой.

∠ABE= ∠ABC/2 =180°/2 =60°

△ABD=△ABE (прямоугольные треугольники с равными острыми углами и общей гипотенузой)

AD=AE = AC/2 =16/2 =8 (см)

Answer 2

Ответ:

8 см

Объяснение:

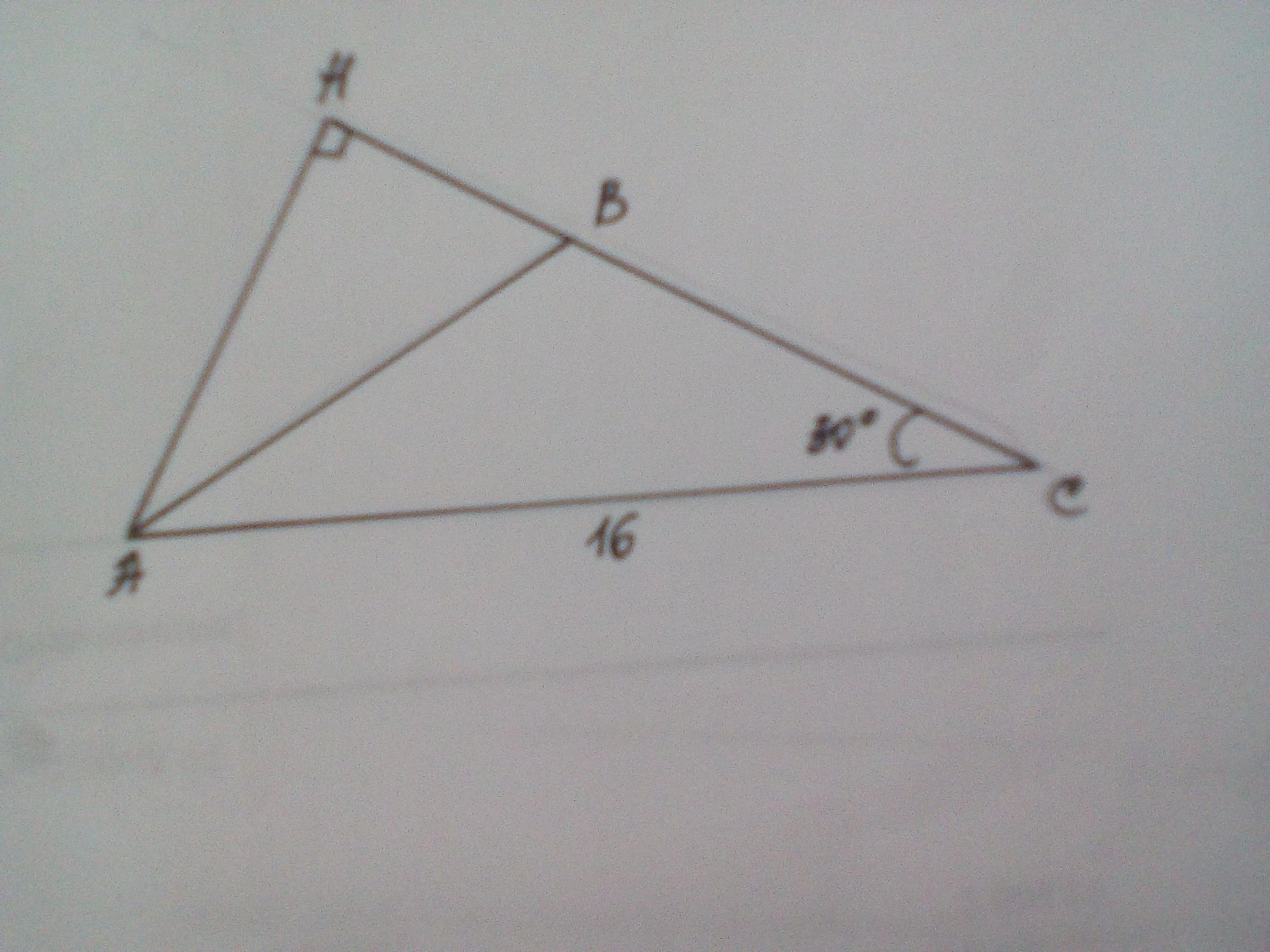
Дано: ΔАВС,  АС=16 см,  ∠В=120°.  АН - высота. Найти АН.

В тупоугольном треугольнике тупой угол является углом при вершине, поэтому

∠АВС=120°,   ∠ВАС=∠АСВ=(180-120):2=30°

В тупоугольном треугольнике высота, проведенная к боковой стороне, падает на её продолжение, поэтому ΔАСН - прямоугольный.

∠С=30°, гипотенуза АС=16 см, значит, АН=16:2=8 см как катет, лежащий против угла 30°.