Question

кут, величина якого 60 градусів, вписано два кола, які зовнішньо дотикаються один до одного. Знайдіть радіус меншого з них, якщо радіус більшого кола 12см.

Answer 1

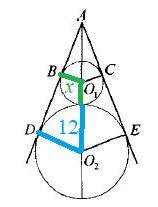
Центры вписанных окружностей О₁ и О₂  лежат на биссектрисе угла А.

Касательная перпендикулярна радиусу, проведенному в точку касания

О₁В ⊥  AD

O₂D ⊥  AD

Пусть r=x; R=12

Катет против угла в 30⁰  равен половине гипотенузы. Значит гипотенуза в два раза больше.

АО₂=24

Прямоугольные треугольники Δ ABО₁  и  Δ ADО₂  подобны по двум углам

Из подобия

О₁В:AO₁=O₂D:AO₂

AO₁=24--12-x=12-x

x:12=(12-x):24   ⇒

x=9