Question

Помогите решить параметр

Answer 1

Ответ: $a$∈[-2; -0.5]

Пошаговое объяснение:

$ax^2 +(1-a^2)x -a > 0$

Рассмотрим 3 случая .

1)

$a>0$

Делим обе части неравенства на a , в этом случае знак неравенства не меняется

$x^2 +\frac{1-a^2}{a} x -1>0$

Поскольку ветви параболы смотрят вверх, в данном случае неравенство либо выполняется при любых действительных x (в случае когда $D<0$), либо при тех x, которые лежат левее наименьшего корня и правее наибольшего корня параболы. ($D>0$, либо если $D=0$ , все x удовлетворяют неравенству помимо единственного корня). Понятно, что в этом случае всегда найдется значение $|x|>2$, что удовлетворяет данному неравенству.

Как видим, этот случай нам не подходит.

2)

$a=0$

$x>0$

Тут, очевидно, также можно взять $|x|>2$ , что удовлетворяет неравенству.

3)

$a<0$

В данном случае, при делении на a, неравенство меняет знак на противоположный.

$x^2 +\frac{1-a^2}{a} x -1<0$

В данном случае, все решения неравенства лежат между корнями параболы, в том случае, если корни существуют  и их ровно два

$D>0$ .  

Таким образом, все решения неравенства по модулю не превосходят двух, в том случае, когда наибольший из корней параболы не превосходит $2$, а наименьший из корней параболы не меньше $-2$, а вершина параболы лежит строго между  -2 и 2. ( Смотрите рисунок)

Таким образом, имеем следующие  условия:

$a<0\\D>0\\f(2) \geq 0\\f(-2)\geq 0\\-2<x_{B} <2$

1. $D>0$

$(\frac{1-a^2}{a} )^2 +4 > 0$

При любом $a<0$

2. $f(2) \geq 0$

$3+ \frac{2(1-a^2)}{a} \geq 0\\\frac{-2a^2+3a+2}{a} \geq 0$

Поскольку $a<0$

$-2a^2+3a+2\leq0\\ 2a^2-3a-2\geq 0\\a_{1} = 2 ; a_{2} = -\frac{1}{2} - teorema vieta\\(a-2)(2a+1) \geq0$

Учитывая, что $a<0$ решением является $a\leq -\frac{1}{2}$

3. $f(-2)\geq 0$

$3- \frac{2(1-a^2)}{a} \geq 0\\\frac{3a-2+2a^2}{a} \geq0\\ 2a^2 +3a-2 \leq 0\\ a_{1} = -2 ; a_{2} = \frac{1}{2} \\(a+2)(2a-1)\leq 0$

Учитывая, что $a<0$ решением является : $-2\leq a<0$

Пересекая с предыдущим решением имеем: $a$∈[-2; -0.5]

4) $-2<x_{B} <2$

$-2<\frac{a^2-1}{2a} < 2$

Поскольку $a<0$

1.

$a^2-1<-4a\\a^2+4a-1<0\\(a+2)^2<5\\-2-\sqrt{5} <a<0$

2.

$a^2-1>4a\\(a-2)^2 >5 \\ a<2-\sqrt{5}$

Таким образом:  $-2-\sqrt{5} <a<2-\sqrt{5}$

пересечем данный промежуток с $a$∈[-2; -0.5].

Очевидно,  что $-2-\sqrt{5} <-2$

Cравним:

$2-\sqrt{5}$ и $-0.5$

$2.5$ и $\sqrt{5}$

Возводим в квадрат:

$6.25>5$

То есть : $2-\sqrt{5} > -0.5$

А значит, пересечение данных промежутков, это сам промежуток  $a$∈[-2; -0.5]  он и является решением.

Answer 2

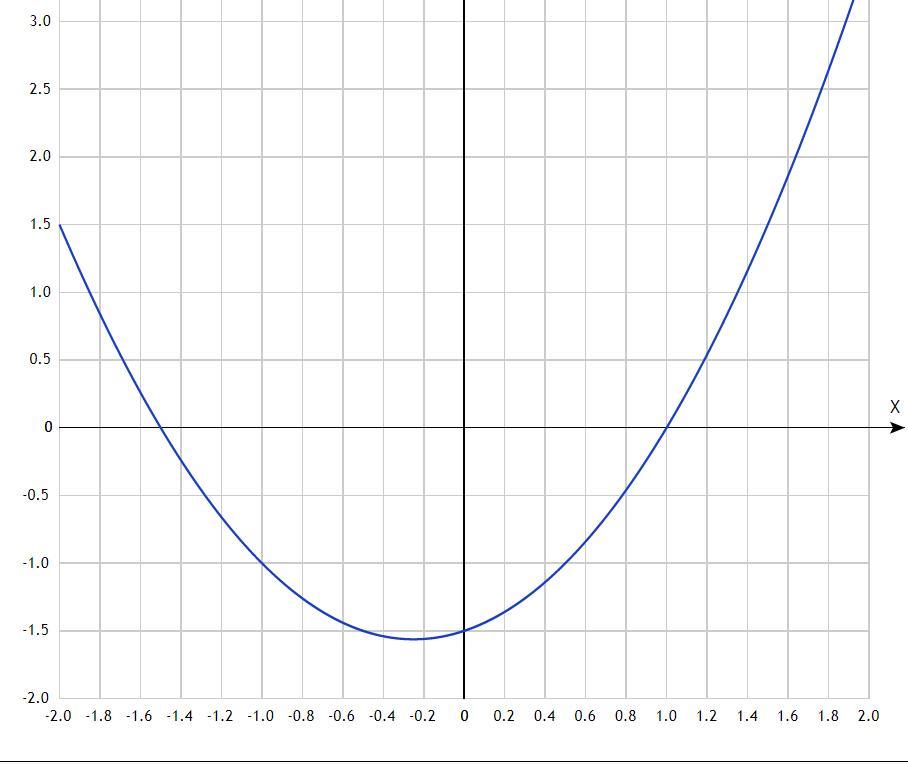
Пошаговое объяснение:см. во вложении