Question

ABC треугольник AC=BC=1 , C угол равен 150 градусов, сторона AB найдите длену​

Answer 1

Ответ:

АВ = √2(√3+1)/2 ед.

Объяснение:

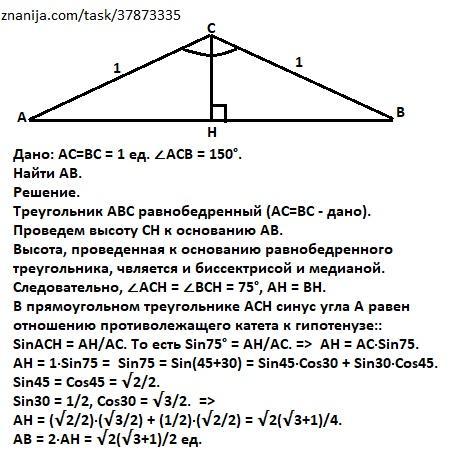
Дано: АС=ВС = 1 ед. ∠АСВ = 150°.

Найти АВ.

Решение.

Треугольник АВС равнобедренный (АС=ВС - дано).

Проведем высоту СН к основанию АВ.

Высота, проведенная к основанию равнобедренного треугольника, является и биссектрисой и медианой.

Следовательно, ∠АСН = ∠ВСН = 75°, АН = ВН.

В прямоугольном треугольнике АСН синус угла А равен отношению противолежащего катета к гипотенузе::

SinACH = АН/АС. То есть Sin75° = АН/АС. =>  AH = AC·Sin75.

AH = 1·Sin75 =  Sin75 = Sin(45+30) = Sin45·Cos30 + Sin30·Cos45.

Sin45 = Cos45 = √2/2.

Sin30 = 1/2, Cos30 = √3/2.  =>

AH = (√2/2)·(√3/2) + (1/2)·(√2/2) = √2(√3+1)/4.

АВ = 2·АН = √2(√3+1)/2 ед.