Question

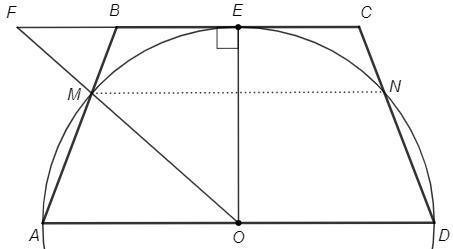
Окружность, построенная на большем основании AD трапеции ABCD как на диаметре, касается меньшего основания и пересекает боковые стороны AB, CD в точках M и N соответственно. Найдите меньшее основание трапеции, если радиус окружности равен 3 и AM:MB=DN:NC=2:1

Answer 1

По обратной теореме Фалеса

AM/DN=MB/NC => AD||MN||BC  

AMND - вписанная трапеция, следовательно равнобедренная. Тогда трапеция ABCD также равнобедренная.  

Радиус в точку касания перпендикулярен касательной, OE⊥BC => OE⊥AD

OE - общий серединный перпендикуляр к основаниям AD и BC, BE=EC  

△AMO~△BMF, AO/BF =AM/BM =MO/MF =2/1

BF=OA/2 =3/2

OF=3/2 OM =9/2

FE =√(OF^2 -OE^2) =√(81/4 -9) = 3√5/2

BC =2BE =2(FE-BF) =3√5 -3