Даю 20 баллов!!!!!
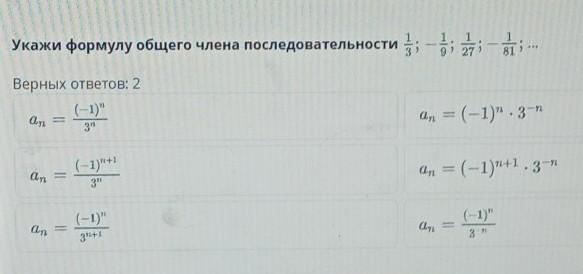
Укажите формулу общего члена последовательности 1/3; - 1/9; 1/27; - 1/87; ...
Приложения:
Ответы
Ответ дал:
2
Ответ:
bottyyy:
спасибо, все правильно
Ответ дал:
2
Это геометрическая прогрессия с первым членом 1/3 и знаменателем прогрессии q = -1/3
или
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад