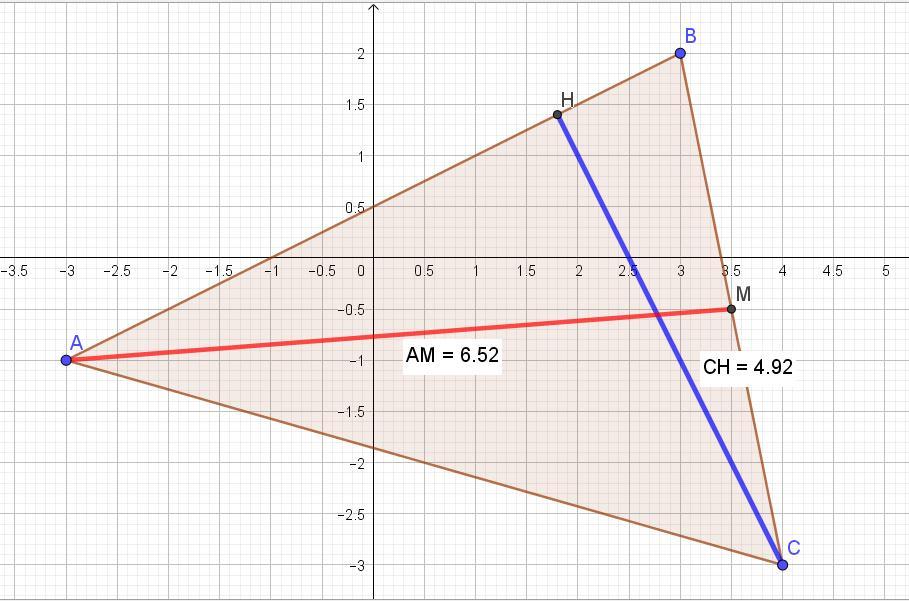
Даны вершины треугольника АВС
Найти:
1) уравнение стороны АВ,
2) уравнение высоты СН и её длины
3) уравнение медианы АМ и её длины
А ( -3;-1) В (3;2) С (4;-3)
Ответы
Даны вершины треугольника АВС : А ( -3;-1), В (3;2,) С (4;-3).
Найти:
1) уравнение стороны АВ.
Вектор АВ = (6; 3).
Уравнение АВ: (х + 3)/6 = (у + 1)/3 каноническое
Сократим знаменатели на 3 и получим общего вида
х - 2у + 1 = 0.
у = (1/2)х + (1/2) с угловым коэффициентом.
2) уравнение высоты СН и её длину .
к(СН) =-1/к(АВ) = -1/(1/2) = -2.
В уравнение у = кх + в подставим данные точки С и к.
-3 = -2*4 + в, отсюда в = - 3 + 8 = 5.
Уравнение СН: у = -2х + 5.
Находим координаты точки Н как точки пересечения СН и АВ.
-2х + 5 = (1/2)х + (1/2),
2,5х = 4,5,
х(Н) = 4,5/2,5 = 9/5 = 1,8.
у(Н) = -2*(9/5) + 5 = (25-18)/5 = 7/5 = 1,4.
Вектор СН = (1,8 - 4; 1,4 -(-3)) = (-2,2; 4,4).
Модуль СН = √((-2,2)² +4,4²) = √24,2 = 4,91935.
3) уравнение медианы АМ и её длину.
Находим координаты точки М .
М((3+4)/2; (2-3)/2) = (3,5; -0,5).
Вектор АМ: (3,5-(-3); -0,5-(-1) = (6,5; 0,5).
Уравнение АМ: (х + 3) / 6,5 = (у + 1) / 0,5
Знаменатели умножим на 2 и получим с целыми коэффициентами:
(х + 3) / 13 = (у + 1) / 1
х + 3 = 13у + 13
х - 13у - 10 = 0.
у = (1/13)х - (10/13).
Модуль АМ = √(6,5² +0,5²) = √42,5 = 6,51920.