Question

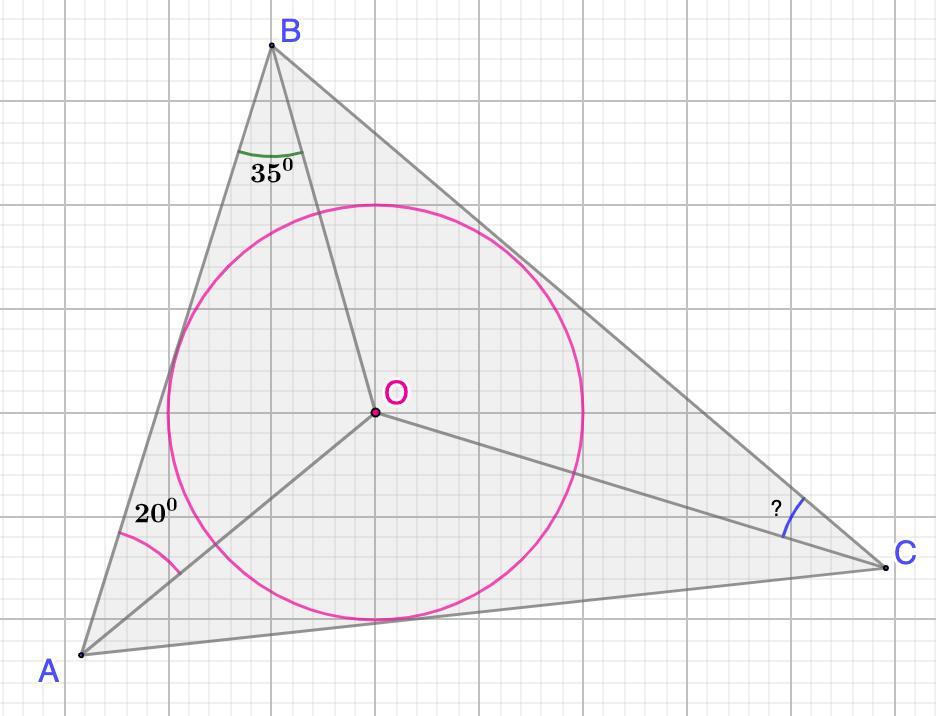
треугольник ABC вписана окружность с центром в точке O, причем ∠BAO = 20°, ∠OBA = 35°. Найди угол ∠BCO. 33° 31° 35°

Answer 1

Ответ:

∠ВСО=35°

Объяснение:

Дано: ΔАВС; окр.О - вписанная;

∠ВАО=20°; ∠ОВА=35°.

Найти: ∠ВСО.

Решение:

Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.

⇒

∠А=2∠ВАО=20°·2=40°

∠В=2∠ОВА=35°·2=70°

∠С=180°-(∠А+∠В)=180°-(40°+70°)=70° (сумма углов Δ-ка 180°)

⇒ ∠ВСО=∠С:2=70°:2=35° (СО - биссектриса)