В выпуклом пятиугольнике ABCD равны 4 стороны : AB=BC =DE=AE .
Углы при вершинах A и B прямые , а при вершине E равен 120 градусов .Найдите угол при вершине C
Ответы
Ответ дал:
0
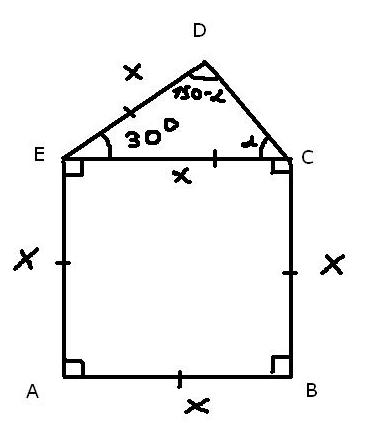
ABCE - квадрат.
Рассмотрим треугольник DCE - он равнобедренный. Угол D
равен углу DCE. По свойству суммы углов треугольника равной
180 градусам. Пусть угол DCE равен  .
.

Так как ABCE - квадрат, то

По условию задачи
Получается, что


Тогда D
 - по свойству суммы углов в треугольнике.
- по свойству суммы углов в треугольнике.





90+75=165 градусов.
Ответ: 165 градусов
Так как ABCE - квадрат, то
По условию задачи
Получается, что
Тогда D
90+75=165 градусов.
Ответ: 165 градусов
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад