Question

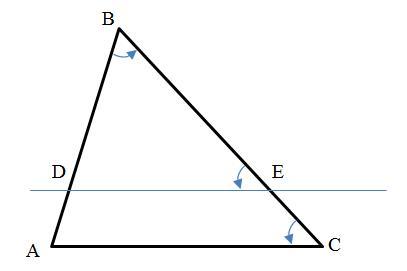
На сторонах AB и BC треугольника ABC отмечены точки D и E соответственно Докажите, что если угол BED = углу BCA , то угол BDE= углу BAC

Answer 1

раз угол BED = углу BCA,то DEпаралельа AC,т.к углы BED и BCA соответственные

так и углы BDE и BAC равны как соответственные

Answer 2

Ответ:

1-й признак подобия треугольников (подобие треугольников по двум углам). Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство.

На сторонах AB и BC треугольника ABC отметим точки D и E, соответственно (см. рисунок). Так как ∠BED = ∠BCA, то треугольники ABC и DBE подобны по первому признаку по углам B и ∠BED = ∠BCA.

У подобных треугольников все углы равны, то есть если для треугольников ABC и DBE имеет место ∠B = ∠B и ∠BED = ∠BCA, то ∠BDE = ∠BAC, что требовалось доказать.