Question

В равнобокой трапеции один из углов равен 120°, диагональ трапеции образует с основанием угол 30°. Найдите большее основание трапеции, если меньшее основание 9см. ПЖ СРОЧНО​

Answer 1

Ответ:

18 см

Объяснение:

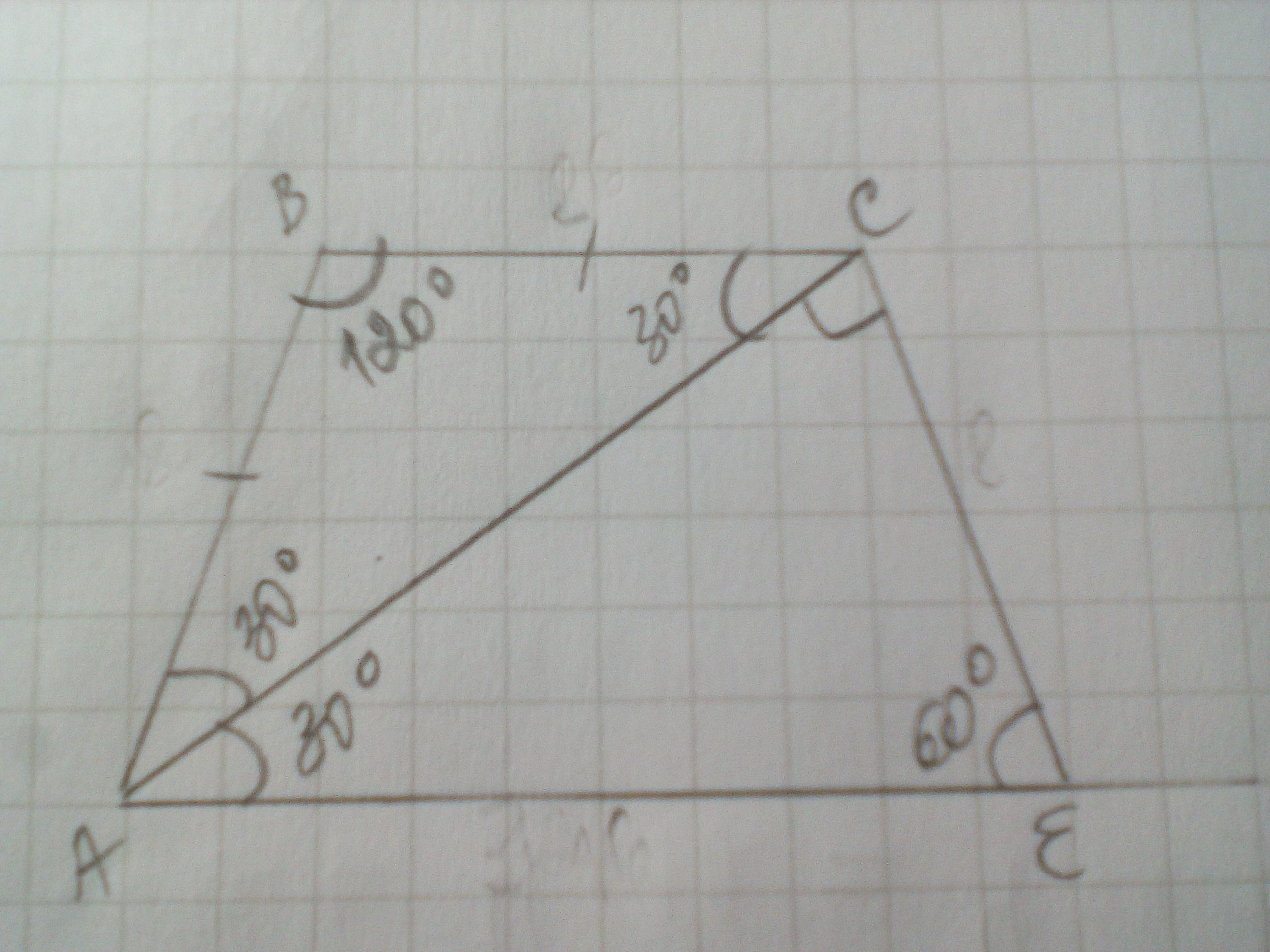
Дано: АВСЕ - трапеция, АВ=СЕ; ВС=9 см; ∠В=120°,  ∠САЕ=30°. Найти АЕ.

Сумма углов трапеции, прилежащих к боковой стороне, составляет 180°.

∠ВАЕ+∠В=180°;  ∠ВАЕ=180-120=60°

∠ВАС=60-30=30°

∠ВСА=180-(120+30)=30°

∠ВАС=∠ВСА,  ΔАВС - равнобедренный, АВ=ВС=СЕ=9 см.

ΔАСЕ; ∠САЕ=1/2 ∠ВАЕ=30°;  ∠Е=60°;  ∠АСЕ=30+60=90°,  ΔАСЕ - прямоугольный

СЕ=1/2 АЕ  по свойству катета, лежащего против угла 30°.

АЕ=9*2=18 см