Question

6. У круговий сектор, радіус якого дорівнює 6 см, а цент-
ральний кут становить 60°, вписано круг. Знайдіть площу цього круга.

Answer 1

Ответ:

4π см²

Объяснение:

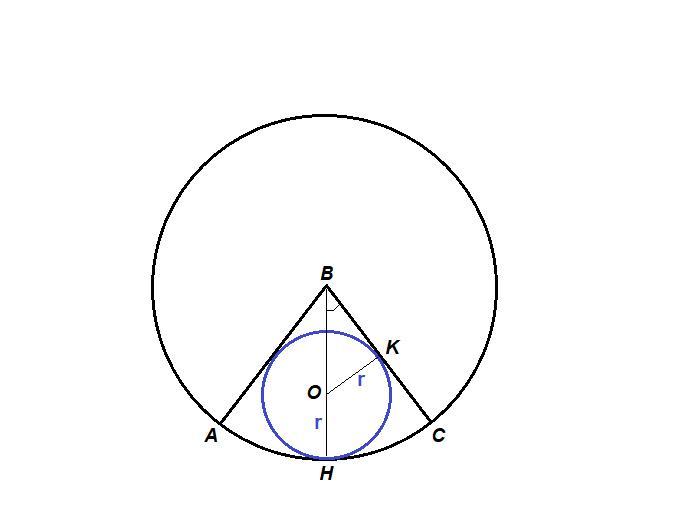
∠АВС = 60°

Круг с центром в точке О вписан в сектор.

Центр круга, вписанного в угол, лежит на биссектрисе угла, тогда

ВО - биссектриса угла АВС,

∠СВН = 1/2 ∠АВС = 30°.

Проведем ОК - радиус в точку касания, тогда ОК ⊥ ВС.

ОК = ОН = r

В прямоугольном треугольнике ОКВ катет ОК лежит против угла в 30°, значит, гипотенуза BO = 2 ОК = 2r.

BH = BO + OH = 2r + r = 3r

ВН = 6 см по условию (радиус сектора)

3r = 6

r = 2 см

Площадь круга:

S = πr² = π · 2² = 4π см²